Calcul dans IR : Exercice 9 2ème année secondaire

Calcul dans IR Problèmes du 1er et du second degré Notion de polynômes Arithmetique Calcul vectoriel Barycentre Translations Homotheties Rotations Suites Fonctions Trigonométrie Géométrie analytique Géométrie dans l'espace Statistiques QCM

78 exercices

Exercice 9 --- (id : 33)

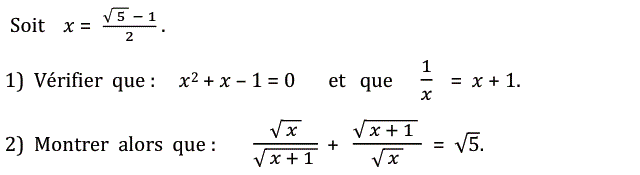
Calcul dans IR: Exercice 9

correction

1)

\left({\frac{\sqrt{5}-1}{2}}\right)^2+\frac{\sqrt{5}-1}{2}-1

=\frac{(\sqrt{5}-1)^2}{4}+\frac{\sqrt{5}-1}{2}-1

=\frac{5-2\sqrt{5}+1}{4}+\frac{2\sqrt{5}-2}{4}-\frac{4}{4}

=\frac{5-2\sqrt{5}+1+2\sqrt{5}-2-4}{4}

=\frac{6-6-2\sqrt{5}+2\sqrt{5}}{4}=0

x^2+x-1=0

équivaut

x(x+1)=1

donc

x+1=\frac{1}{x}

car

x\neq 0

2)

x+1=\frac{1}{x}

équivaut

\frac{x+1}{x}=\frac{1}{x^2}

(x>0)

équivaut

\sqrt{\frac{x+1}{x}}=\sqrt{\frac{1}{x^2}}

équivaut

\frac{\sqrt{x+1}}{\sqrt{x}}=\frac{1}{x}

et

\frac{\sqrt{x}}{\sqrt{x+1}}=x

Donc

\frac{\sqrt{x+1}}{\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x+1}}

=\frac{1}{x}+x=(x+1)+x

=2x+1=2\frac{\sqrt{5}-1}{2}+1

=\sqrt{5}-1+1=\sqrt{5}

<< < 1...456789 1011121314...19...29 > >>