Calcul dans IR : Exercice 11 2ème année secondaire
Calcul dans IRProblèmes du 1er et du second degréNotion de polynômesArithmetiqueCalcul vectorielBarycentreTranslationsHomothetiesRotationsSuitesFonctionsTrigonométrieGéométrie analytiqueGéométrie dans l'espaceStatistiquesQCM
78 exercices
Exercice 11 --- (id : 10)
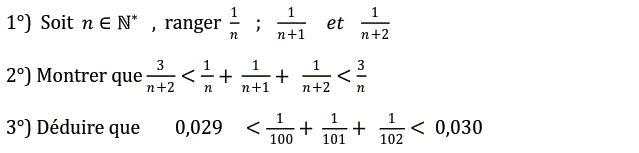
correction
1)
Pour tout entier naturel n non nul on sait que $n< n+1 < n+2$ donc $\dfrac{1}{n}>\dfrac{1}{n+1}>\dfrac{1}{n+2}$ ou encore
$\dfrac{1}{n+2}<\dfrac{1}{n+1}<\dfrac{1}{n}$
$\dfrac{1}{n+2}<\dfrac{1}{n+1}<\dfrac{1}{n}$
2)
$\dfrac{1}{n+2}<\dfrac{1}{n}\leqslant \dfrac{1}{n}$
$\dfrac{1}{n+2}<\dfrac{1}{n+1}<\dfrac{1}{n}$
$\dfrac{1}{n+2}\leqslant \dfrac{1}{n+2}<\dfrac{1}{n}$
En faisant la somme membre à membre des trois encadrements précédents , on obtient:
$\dfrac{3}{n+2}<\dfrac{1}{n}+\dfrac{1}{n+1}+\dfrac{1}{n+2}<\dfrac{3}{n}$
$\dfrac{1}{n+2}<\dfrac{1}{n+1}<\dfrac{1}{n}$
$\dfrac{1}{n+2}\leqslant \dfrac{1}{n+2}<\dfrac{1}{n}$
En faisant la somme membre à membre des trois encadrements précédents , on obtient:
$\dfrac{3}{n+2}<\dfrac{1}{n}+\dfrac{1}{n+1}+\dfrac{1}{n+2}<\dfrac{3}{n}$
3)
Il suffit de choisir $n=100$ et d'appliquer l'encadrement précédent.