Calcul dans IR : Exercice 10 2ème année secondaire
Calcul dans IRProblèmes du 1er et du second degréNotion de polynômesArithmetiqueCalcul vectorielBarycentreTranslationsHomothetiesRotationsSuitesFonctionsTrigonométrieGéométrie analytiqueGéométrie dans l'espaceStatistiquesQCM
78 exercices
Exercice 10 --- (id : 9)
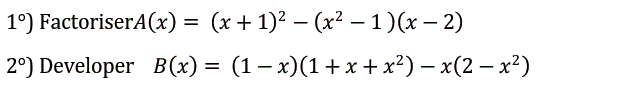
correction
1)
$A(x)=(x+1)^2-(x^2-1)(x-2)$
$=(x+1)^2-(x+1)(x-1)(x-2)$
$=(x+1)\left[{(x+1)-(x-1)(x-2)}\right]$ $=(x+1)\left[{x+1-(x^2-3x+2)}\right]$
$=(x+1)(x+1-x^2+3x-2)$ $=(x+1)(-x^2+4x-1)$
On peut aussi factoriser le 2ème facteur de la façon suivante.
$A(x)=-(x+1)(x^2-4x+1)$
$=(x+1)\left[{(x^2-4x+4)-3}\right]$ $=(x+1)\left[{(x-2)^2-(\sqrt{3})^2}\right]$
$=(x+1)(x-2-\sqrt{3})(x-2+\sqrt{3})$
$=(x+1)\left[{(x+1)-(x-1)(x-2)}\right]$ $=(x+1)\left[{x+1-(x^2-3x+2)}\right]$
$=(x+1)(x+1-x^2+3x-2)$ $=(x+1)(-x^2+4x-1)$
On peut aussi factoriser le 2ème facteur de la façon suivante.
$A(x)=-(x+1)(x^2-4x+1)$
$=(x+1)\left[{(x^2-4x+4)-3}\right]$ $=(x+1)\left[{(x-2)^2-(\sqrt{3})^2}\right]$
$=(x+1)(x-2-\sqrt{3})(x-2+\sqrt{3})$
2)
$B(x)=(1-x)(1+x+x^2)-x(2-x^2)$
$=1+x+x^2-x-x^2-x^3-2x+x^3$
$=1-2x$
$=1+x+x^2-x-x^2-x^3-2x+x^3$
$=1-2x$