Activités numériques I : Exercice 4 première année secondaire
Activités numériques IActivités numériques IIActivités algébriquesFonctions linéairesEquations et inéquationsFonctions affinesSystème de deux équationsStatistiquesAnglesThalesRapports trigonométriqueVecteurs et translationsActivités dans un repereQuart de tourSections planes solideQCM
88 exercices
Exercice 4 --- (id : 1005)
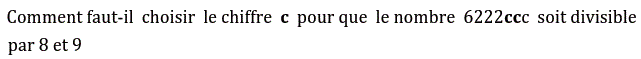
correction
Soit c un entier naturel tel que 0≤c≤9.
Le nombre 6222ccc est divisible par 8 et 9
équivaut 100c+10c+c est divisible par 8 et 6+2+2+2+c+c+c est divisible par 9
équivaut 111c est divisible par 8 et 3c+12 est divisible par 9
équivaut 104c+7c est divisible par 8 et 3c+9+3 est divisible par 9
équivaut 7c est divisible par 8 et 3(c+1) est divisible par 9 (car 104c=8×13c divisible par 8)
équivaut 7c est divisible par 8 et c+1 est divisible par 3
c+1 est divisible par 3 équivaut $c\in \left\{{2,5,8}\right\}$.
Pour c=2 on a: 7c=14 n'est pas divisible par 8
Pour c=5 on a:7c=35 n'est pas divisible par 8
Pour c=8 on a:7c=7×8 divisible par 8
$\boxed{Conclusion:} $ Le nombre 6222ccc est divisible par 8 et 9 si et seulement si c=8.
Le nombre 6222ccc est divisible par 8 et 9
équivaut 100c+10c+c est divisible par 8 et 6+2+2+2+c+c+c est divisible par 9
équivaut 111c est divisible par 8 et 3c+12 est divisible par 9
équivaut 104c+7c est divisible par 8 et 3c+9+3 est divisible par 9
équivaut 7c est divisible par 8 et 3(c+1) est divisible par 9 (car 104c=8×13c divisible par 8)
équivaut 7c est divisible par 8 et c+1 est divisible par 3
c+1 est divisible par 3 équivaut $c\in \left\{{2,5,8}\right\}$.
Pour c=2 on a: 7c=14 n'est pas divisible par 8
Pour c=5 on a:7c=35 n'est pas divisible par 8
Pour c=8 on a:7c=7×8 divisible par 8
$\boxed{Conclusion:} $ Le nombre 6222ccc est divisible par 8 et 9 si et seulement si c=8.