Probabilité conditionnelle
Dhaouadi Nejib
⚜
I. Définition
Activité
Une urne contient cept boules noires numérotées 0,0,0,0,1,1,1 et cinq boules blanches numérotées 0,0,1,1,1.
Toutes les boules sont indiscernables au toucher.
1) On tire une boule au hasard et on considère les événements suivants:
N : "La boule tirée est noire"
A : "La boule tirée porte le numéro 0"
Calculer les probabilités p(N), p(A) et p(N∩A)
2) On a tiré une boule de l'urne, on a remarqué qu'elle est noire.
Calculer la probabilité q que la boule tirée porte le numéro 0.
Comparer q et $\frac{p(N∩A)}{p(N)}$.
1) On tire une boule au hasard et on considère les événements suivants:
N : "La boule tirée est noire"
A : "La boule tirée porte le numéro 0"
Calculer les probabilités p(N), p(A) et p(N∩A)
2) On a tiré une boule de l'urne, on a remarqué qu'elle est noire.
Calculer la probabilité q que la boule tirée porte le numéro 0.
Comparer q et $\frac{p(N∩A)}{p(N)}$.
Solutions ✍
Le contenu de l'urne peut être résumé dans le tableau suivant:
1) L'univers E des cas possibles est formé par les 12 boules donc
$p(N)=\frac{Card(N)}{Card(E)}=\frac{7}{12}$; $p(A)=\frac{Card(A)}{Card(E)}=\frac{6}{12}=\frac{1}{2}$
N∩A : "La boule tirée est noire n° 0"
Donc $p(N∩A)=\frac{card(N∩A)}{Card(E)}=\frac{4}{12}=\frac{1}{3}$
2) Dans ce cas un cas possible est forcément une boule noire (car on sait dèja quelle est noire) donc l'univers des cas possibles se réduit à l'ensemble des cept boules noires seulement.
Donc $q=\frac{4}{7}$ et $\frac{p(N∩A)}{p(N)}=\frac{\frac{1}{3}}{\frac{7}{12}}=\frac{1}{3}.\frac{12}{7}=\frac{4}{7}=q$
Commentaire: q est appelé probabilité conditionnelle de A sachant N.
| Boules noires | Boules blanches | |
| Boules n° 0 | 4 | 2 |
| Boules n° 1 | 3 | 3 |
N∩A : "La boule tirée est noire n° 0"
Donc $p(N∩A)=\frac{card(N∩A)}{Card(E)}=\frac{4}{12}=\frac{1}{3}$
2) Dans ce cas un cas possible est forcément une boule noire (car on sait dèja quelle est noire) donc l'univers des cas possibles se réduit à l'ensemble des cept boules noires seulement.
Donc $q=\frac{4}{7}$ et $\frac{p(N∩A)}{p(N)}=\frac{\frac{1}{3}}{\frac{7}{12}}=\frac{1}{3}.\frac{12}{7}=\frac{4}{7}=q$
Commentaire: q est appelé probabilité conditionnelle de A sachant N.
Théorème et définition
Soit $(E,{\scr{P}}(E),p)$ un espace probabilisé fini.
Soit B un événement tel que $p(B)\neq 0$
L'application $p_B$ définie de ${\scr{P}}(E)$ sur $\left[{0,1}\right]$ par : $p_B(A)=\frac{p(A∩B)}{p(B)}$ est une probabilité.
La probabilité $p_B$ est appelée probabilité B-conditionnelle
Le réel $p_B(A)$ noté aussi $p(A/B)$ est appelé probabilité conditionnelle de A sachant que B est réalisé ou tout simplement probabilité de A sachant B.
Soit B un événement tel que $p(B)\neq 0$
L'application $p_B$ définie de ${\scr{P}}(E)$ sur $\left[{0,1}\right]$ par : $p_B(A)=\frac{p(A∩B)}{p(B)}$ est une probabilité.
La probabilité $p_B$ est appelée probabilité B-conditionnelle
Le réel $p_B(A)$ noté aussi $p(A/B)$ est appelé probabilité conditionnelle de A sachant que B est réalisé ou tout simplement probabilité de A sachant B.
Démonstration
✎ Montrons que $p_B$ est une probabilité- $p_B(E)=\frac{p(E∩B)}{p(B)}=\frac{p(B))}{p(B)}=1$
- $p_B(∅)=\frac{p(∅∩B)}{p(B)}=\frac{p(∅))}{p(B)}=0$
- Soit A un événement
On pose A={$a_1,a_2,...,a_n$}=$\{a_1\}∪\{a_2\}∪ ... ∪\{a_n\}$ $=\bigcup\limits_{i=1}^{n}\{a_i\}$
$p_B(A)=\frac{p(A∩B)}{p(B)}$$=\frac{p\left({\left({\bigcup\limits_{i=1}^{n}\{a_i\}}\right)∩B}\right)}{p(B)}$ $=\frac{p\left({\bigcup\limits_{i=1}^{n}\left({\{a_i\}∩B}\right)}\right)}{p(B)}$
Or les événements $\{a_1\}∩B,\{a_2\}∩B, ... , \{a_n\}∩B $ sont deux à deux incompatibles car $\{a_i\}∩B=\{a_i\}$ ou $\{a_i\}∩B=∅$
Donc $p_B(A)=\frac{\sum\limits_{i=1}^{n}p\left({\{a_i\}∩B}\right)}{p(B)}$ $=\sum\limits_{i=1}^{n}\frac{p\left({\{a_i\}∩B}\right)}{p(B)}=\sum\limits_{i=1}^{n}p_B\left({\{a_i\}}\right)$
Exemple 1
Dans un lycée, on demande aux élèves et aux professeurs s’ils préfèrent avoir cours le matin ou l’après-midi.
On obtient les résultats donnés dans le tableau ci-dessous :
On choisit une personne au hasard (parmi élèves et professeurs) et on considère les événements :
E : « La personne tirée au sort est un élève »
M : « La personne tirée au sort préfère avoir cours le matin ».
1) Calculer p(E) et p(E∩M)
2) En déduire P(M/E) avec la formule de la définition précédente.
3) Retrouver ce résultat sans utiliser la formule du cours.
On obtient les résultats donnés dans le tableau ci-dessous :
| Matin | Après-midi | Total | |
| Élèves | 657 | 438 | 1095 |
| Profs | 84 | 21 | 105 |
| Total | 741 | 459 | 1200 |
E : « La personne tirée au sort est un élève »
M : « La personne tirée au sort préfère avoir cours le matin ».
1) Calculer p(E) et p(E∩M)
2) En déduire P(M/E) avec la formule de la définition précédente.
3) Retrouver ce résultat sans utiliser la formule du cours.
Solutions ✍
1) On est dans une situation d'équiprobabilité donc
p(E)=$\frac{1095}{1200}=0,9125$ et p(E∩M)=$\frac{657}{1200}=0,5475$
2) p(M/E)=$\frac{p(M∩E)}{p(E)}=\frac{0,5475}{0,9125}=0,6$
3) On sait que la personne choisie est un élève donc l'univers se réduit à l'ensemble des élèves seulement (on s'interesse seulement à la première ligne du tableau) donc
p(M/E)=$\frac{657}{1095}=0,6$
p(E)=$\frac{1095}{1200}=0,9125$ et p(E∩M)=$\frac{657}{1200}=0,5475$
2) p(M/E)=$\frac{p(M∩E)}{p(E)}=\frac{0,5475}{0,9125}=0,6$
3) On sait que la personne choisie est un élève donc l'univers se réduit à l'ensemble des élèves seulement (on s'interesse seulement à la première ligne du tableau) donc
p(M/E)=$\frac{657}{1095}=0,6$
Propriété
Soit $(E,{\scr{P}}(E),p)$ un espace probabilisé fini.
A et B deux événements tels que p(A)≠0 et p(B)≠0
$p(A∩B)=p(B)×p(A/B)$$=p(A)×p(B/A)$
Cette formule est appelée Formule des probabilités composées
A et B deux événements tels que p(A)≠0 et p(B)≠0
$p(A∩B)=p(B)×p(A/B)$$=p(A)×p(B/A)$
Cette formule est appelée Formule des probabilités composées
Remarques
La formule des probabilités composées peut s'étendre à trois événements A, B et C tels que p(A)≠0 et p(A∩B)≠0 de la façon suivante:$p(A∩B∩C)$ $=p(A)×p(B/A)×p(C/A∩B)$
Exemple 2
Une urne contient cept boules noires et cinq boules blanches.
Toutes les boules sont indiscernables au toucher.
On tire successivement et sans remise (sans remettre à chaque fois la boule tirée dans l'urnes) trois boules de l'urne,
Déterminer les probabilité des événements suivants:
A : "La première boule noire apparait au troisième tirage."
B : "Seulement, les deux dernières boules tirées sont de même couleur."
Toutes les boules sont indiscernables au toucher.
On tire successivement et sans remise (sans remettre à chaque fois la boule tirée dans l'urnes) trois boules de l'urne,
Déterminer les probabilité des événements suivants:
A : "La première boule noire apparait au troisième tirage."
B : "Seulement, les deux dernières boules tirées sont de même couleur."
Solutions ✍
Considérons les événements suivants
$N_i$ : "La boule tirée au i-ème tirage est noire." avec 1≤i≤3
$B_i$ : "La boule tirée au i-ème tirage est blanche." avec 1≤i≤3
A est réalisé si les boules tirées sont dans l'ordre :
boule blanche au premier tirage, boule blanche au deuxième tirage et puis boule noire au troisième tirage. Donc on peut écrire
$p(A)= p(B_1∩B_2∩N_3)$ $= p(B_1)×p(B_2/B_1)×p(N_3/B_1∩B_2)$ $= \frac{5}{12}×\frac{4}{11}×\frac{7}{10}≈0,11$
B est réalisé si les boules tirées sont dans l'ordre :
boule blanche au premier tirage, boule noire au deuxième tirage et puis boule noire au troisième tirage ou boule noire au premier tirage, boule blanche au deuxième tirage et puis boule blanche au troisième tirage. Donc on peut écrire $p(B)= p(\left({B_1∩B_2∩N_3}\right)∪\left({N_1∩N_2∩B_3}\right))$ $= p(B_1)×p(B_2/B_1)×p(N_3/B_1∩B_2)$ $+p(N_1)×p(N_2/N_1)×p(B_3/N_1∩N_2)$ $=\frac{5}{12}×\frac{4}{11}×\frac{7}{10}+\frac{7}{12} ×\frac{6}{11}×\frac{5}{10}$ $=0,265152$
$N_i$ : "La boule tirée au i-ème tirage est noire." avec 1≤i≤3
$B_i$ : "La boule tirée au i-ème tirage est blanche." avec 1≤i≤3
A est réalisé si les boules tirées sont dans l'ordre :
boule blanche au premier tirage, boule blanche au deuxième tirage et puis boule noire au troisième tirage. Donc on peut écrire
$p(A)= p(B_1∩B_2∩N_3)$ $= p(B_1)×p(B_2/B_1)×p(N_3/B_1∩B_2)$ $= \frac{5}{12}×\frac{4}{11}×\frac{7}{10}≈0,11$
B est réalisé si les boules tirées sont dans l'ordre :
boule blanche au premier tirage, boule noire au deuxième tirage et puis boule noire au troisième tirage ou boule noire au premier tirage, boule blanche au deuxième tirage et puis boule blanche au troisième tirage. Donc on peut écrire $p(B)= p(\left({B_1∩B_2∩N_3}\right)∪\left({N_1∩N_2∩B_3}\right))$ $= p(B_1)×p(B_2/B_1)×p(N_3/B_1∩B_2)$ $+p(N_1)×p(N_2/N_1)×p(B_3/N_1∩N_2)$ $=\frac{5}{12}×\frac{4}{11}×\frac{7}{10}+\frac{7}{12} ×\frac{6}{11}×\frac{5}{10}$ $=0,265152$
●
Formule des probabilités totales
Propriété
Soit $(E,{\scr{P}}(E),p)$ un espace probabilisé fini.
A et B deux événements tels que p(B)≠0 et p(B)≠1
$p(A)= p(A∩B)+p(A∩\overline{B})$ $= p(B)×p(A/B)+p(\overline{B})×p(A/\overline{B})$
D’une manière plus générale, si $B_1, B_2, . . . et\ B_n$ forment un système complet de l'univers E (c-à-d deux à deux incompatibles et tels que $B_1∪B_2∪...∪B_n=E$) et de probabilités non nulles alors pour tout événement A:
$p(A)= \sum\limits_{i=1}^n p(A∩B_i)$ $= \sum\limits_{i=1}^n p(B_i)×p(A/B_i)$
A et B deux événements tels que p(B)≠0 et p(B)≠1
$p(A)= p(A∩B)+p(A∩\overline{B})$ $= p(B)×p(A/B)+p(\overline{B})×p(A/\overline{B})$
D’une manière plus générale, si $B_1, B_2, . . . et\ B_n$ forment un système complet de l'univers E (c-à-d deux à deux incompatibles et tels que $B_1∪B_2∪...∪B_n=E$) et de probabilités non nulles alors pour tout événement A:
$p(A)= \sum\limits_{i=1}^n p(A∩B_i)$ $= \sum\limits_{i=1}^n p(B_i)×p(A/B_i)$
Démonstration
$A=A∩E=A∩(B∪\overline{B})$ $=(A∩B)∪(A∩\overline{B})$ avec $(A∩B)∩(A∩\overline{B})=∅$
Donc $p(A)=p(A∩B)+p(A∩\overline{B})$ $=p(B)×p(A/B)+p(\overline{B})×p(A/\overline{B})$ (probabilités composées)
De même on a : $A=A∩E=A∩(\bigcup\limits_{i=1}^{n}{B_i})=\bigcup\limits_{i=1}^{n}{(A∩B_i)}$ ce qui donne $p(A)=\sum\limits_{i=1}^{n}{p(A∩B_i)}$ $=\sum\limits_{i=1}^{n}p(B_i)×p(A/B_i)$ car les événements $A∩B_i$ sont 2 à 2 incompatibles
Donc $p(A)=p(A∩B)+p(A∩\overline{B})$ $=p(B)×p(A/B)+p(\overline{B})×p(A/\overline{B})$ (probabilités composées)
De même on a : $A=A∩E=A∩(\bigcup\limits_{i=1}^{n}{B_i})=\bigcup\limits_{i=1}^{n}{(A∩B_i)}$ ce qui donne $p(A)=\sum\limits_{i=1}^{n}{p(A∩B_i)}$ $=\sum\limits_{i=1}^{n}p(B_i)×p(A/B_i)$ car les événements $A∩B_i$ sont 2 à 2 incompatibles
Exemple 3
Dans une ville, 40% de la population a les cheveux blonds, 50% les yeux bleus et 35% les cheveux blonds et les yeux bleus. On choisit une personne au hasard.
Quelle est la probabilité :
1) pour qu’elle ait les yeux bleus, sachant qu’elle a les cheveux blonds ?
2) pour qu’elle n’ait pas les cheveux blonds, sachant qu’elle a les yeux bleus ?
Quelle est la probabilité :
1) pour qu’elle ait les yeux bleus, sachant qu’elle a les cheveux blonds ?
2) pour qu’elle n’ait pas les cheveux blonds, sachant qu’elle a les yeux bleus ?
Solutions ✍
Considérons les événements :
C : "La personne choisie a les cheveux blonds".
O : "La personne choisie a les yeux bleus".
1) $p(O/C)=\frac{p(O∩C)}{p(C)}=\frac{0,35}{0,40}$ $=\frac{35}{40}=\frac{7}{8}=0,875$
2) $p(\overline{C}/O)=\frac{p(\overline{C}∩O)}{p(O)}$ or d'après la formule des probabilités totales on sait que $p(O)=p(C∩O)+p(\overline{C}∩O)$ ce qui donne $p(\overline{C}∩O)=p(O)-p(C∩O))$ $=0,5-0,35=0,15$
Donc $p(\overline{C}/O)=\frac{0,15}{0,5}=\frac{15}{50}=\frac{3}{10}=0,3$
C : "La personne choisie a les cheveux blonds".
O : "La personne choisie a les yeux bleus".
1) $p(O/C)=\frac{p(O∩C)}{p(C)}=\frac{0,35}{0,40}$ $=\frac{35}{40}=\frac{7}{8}=0,875$
2) $p(\overline{C}/O)=\frac{p(\overline{C}∩O)}{p(O)}$ or d'après la formule des probabilités totales on sait que $p(O)=p(C∩O)+p(\overline{C}∩O)$ ce qui donne $p(\overline{C}∩O)=p(O)-p(C∩O))$ $=0,5-0,35=0,15$
Donc $p(\overline{C}/O)=\frac{0,15}{0,5}=\frac{15}{50}=\frac{3}{10}=0,3$
Exemple 4
Lors d’un concours la première épreuve est une épreuve de mathématiques, la deuxième épreuve est une épreuve de sciences physiques.
Un élève a 80% de chance de réussir la première épreuve, s’il réussit la première épreuve il aura 75% de chance de réussir la deuxième épreuve, et s’il ne réussit pas la première épreuve il aura 40% de chance de réussir la deuxième épreuve.
On désigne par M l’événement « l’élève réussit la première épreuve » et par S l’événement « l’élève réussit la deuxième épreuve ».
Déterminer $p(M),\ p(S/M),\ p(S/\overline{M}) \ et \ p(S)$
Un élève a 80% de chance de réussir la première épreuve, s’il réussit la première épreuve il aura 75% de chance de réussir la deuxième épreuve, et s’il ne réussit pas la première épreuve il aura 40% de chance de réussir la deuxième épreuve.
On désigne par M l’événement « l’élève réussit la première épreuve » et par S l’événement « l’élève réussit la deuxième épreuve ».
Déterminer $p(M),\ p(S/M),\ p(S/\overline{M}) \ et \ p(S)$
Solutions ✍
D'après les données on a: $p(M)=\frac{80}{100}=0,8$ , $p(S/M)=\frac{75}{100}=0,75$ et $p(S/\overline{M})=\frac{40}{100}=0,4$
D'après la formule des probabilités totales on a: $p(S)=p(S∩M)+p(S∩\overline{M})$ $=p(M)×p(S/M)$ $+p(\overline{M})×p(S/\overline{M})$ $=0,8×0,75+(1-0,8)×0,4=0,68$
D'après la formule des probabilités totales on a: $p(S)=p(S∩M)+p(S∩\overline{M})$ $=p(M)×p(S/M)$ $+p(\overline{M})×p(S/\overline{M})$ $=0,8×0,75+(1-0,8)×0,4=0,68$
⚜
II. Arbre pondéré
On peut représenter une situation par un arbre pondéré.
- La probabilité d’un événement correspondant à un chemin est égale au produit des probabilités inscrites sur chaque branche de ce chemin (Règle qui reflète la formule des probabilités composées)
- la probabilité d’un évènement est la somme des probabilités associées aux chemins qui permettent de réaliser cet évènement (Règle qui reflète la formule des probabilités totales)
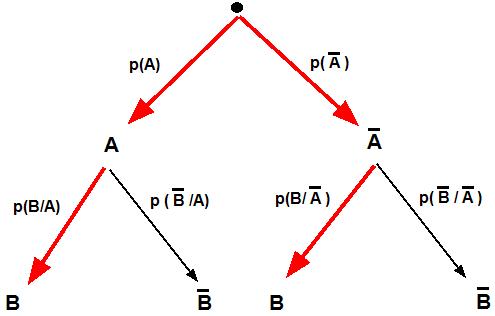
Interprétation
- L'événement A∩B est représenté par le chemin : $\bullet \to A \to B$
La probabilité de ce chemin est le produit des probabilités des branches, ce qui exprime $p(A∩B)=p(A)×p(B/A)$
De même pour les autres chemins:
$A∩\overline{B}$ représenté par le chemin $\bullet \to A \to \overline{B}$
$\overline{A}∩B$ représenté par le chemin $\bullet \to \overline{A} \to B$
$\overline{A}∩\overline{B}$ représenté par le chemin $\bullet \to \overline{A} \to \overline{B}$ - La probabilité de B est la somme des probabilités associées aux chemins qui permettent de réaliser cet évènement (les chemins $\bullet \to A \to B$ et $\bullet \to \overline{A} \to B$).
Ce qui donne $p(B)=p(A∩B)+p(\overline{A}∩B)$ - La règle des nœuds exige les égalités suivantes:
$p(A)+p(\overline{A})=1$
$p(B/A)+p(\overline{B}/A)=1$
$p(B/\overline{A})+p(\overline{B}/\overline{A})=1$
Exemple 5
Un fabricant d'ampoules possède deux machines A et B. La machine A fournit 65% de la production, et la machine B fournit le reste.
Certains ampoules présentent un défaut de fabrication:
- à la sortie de la machine A, 8% des ampoules présentent un défaut;
- à la sortie de la machine B, 5% des ampoules présentent un défaut.
On définie les événements suivants:
A: "l'ampoule provient de la machine A"
B: "l'ampoule provient de la machine B"
D: "l'ampoule présente un défaut"
On prélève une ampoule au hasard parmi la production totale d'une journée.
1) Construire un arbre pondérée présentant la situation
2) Montrer que la probabilité de tirer une ampoule sans défaut est égale à 0,9305
3) L'ampoule est sans défaut.
Calculer la probabilité qu'elle provienne de la machine A.
Certains ampoules présentent un défaut de fabrication:
- à la sortie de la machine A, 8% des ampoules présentent un défaut;
- à la sortie de la machine B, 5% des ampoules présentent un défaut.
On définie les événements suivants:
A: "l'ampoule provient de la machine A"
B: "l'ampoule provient de la machine B"
D: "l'ampoule présente un défaut"
On prélève une ampoule au hasard parmi la production totale d'une journée.
1) Construire un arbre pondérée présentant la situation
2) Montrer que la probabilité de tirer une ampoule sans défaut est égale à 0,9305
3) L'ampoule est sans défaut.
Calculer la probabilité qu'elle provienne de la machine A.
Solutions ✍
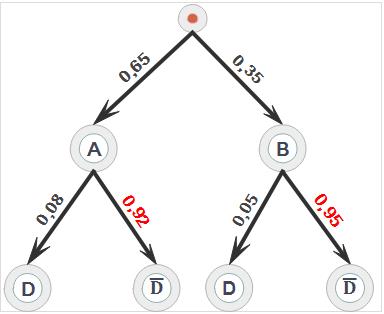 2)
D'après la formule des probabilités totales on a:
2)
D'après la formule des probabilités totales on a:
$p(\overline D)=p(A\cap \overline D)+p(B \cap \overline D)$ $=p(A) \times p(\overline D /A) $ $+ p(B) \times p(\overline D /B)$ $=0,65 \times 0,92 + 0,35 \times 0,95$ $ = 0,9305$
3) $p(A/\overline D) =\frac{p(A \cap \overline D)}{p(\overline D)}$ $=\frac{p(A) \times p(\overline D/A)}{p(\overline D)}$ $=\frac{0,65 \times 0,92}{0,9305}\simeq 0,643$
1)

$p(\overline D)=p(A\cap \overline D)+p(B \cap \overline D)$ $=p(A) \times p(\overline D /A) $ $+ p(B) \times p(\overline D /B)$ $=0,65 \times 0,92 + 0,35 \times 0,95$ $ = 0,9305$
3) $p(A/\overline D) =\frac{p(A \cap \overline D)}{p(\overline D)}$ $=\frac{p(A) \times p(\overline D/A)}{p(\overline D)}$ $=\frac{0,65 \times 0,92}{0,9305}\simeq 0,643$
Exemple 6
Pierre et Claude jouent au Tennis. Les deux joueurs ont la même chance de gagner la première partie. Par la suite, lorsque Pierre gagne une partie, la probabilité qu'il gagne la suivante est 0,7. Et s'il perd une partie, la probabilité qu'il perde la suivante est 0,8.
Dans la suite n est un entier naturel non nul.
On considère les événements :
Gn : "Pierre gagne la n-ième partie"
Pn : "Pierre perd la n-ième partie"
On pose pn=p(Gn) et qn = p(Pn)
1) Recherche d'une relation de récurrence.
░░a) Déterminer $p_1$ puis $p(G_2/G_1)$ et $p(G_2/P_1)$.
░░b) Construire un arbre pondérée qui exprime les deux premières parties et calculer $p(G_2)$
░░c) Justifier l'égalité $p_n+q_n=1$.
░░d) Démontrer que pour tout entier naturel non nul n; $p_{n+1}=0,5p_n+0,2$
2) Etude de la suite $(p_n)$
On pose pour tout entier naturel n non nul, $v_n=p_n-0,4$
░░a) Prouver que $(v_n)$ est une suite géométrique et exprimer $v_n$ en fonction de n.
░░b) En déduire $p_n$ en fonction de n et déterminer $\lim\limits_{n \to +\infty}{p_n}$.
Dans la suite n est un entier naturel non nul.
On considère les événements :
Gn : "Pierre gagne la n-ième partie"
Pn : "Pierre perd la n-ième partie"
On pose pn=p(Gn) et qn = p(Pn)
1) Recherche d'une relation de récurrence.
░░a) Déterminer $p_1$ puis $p(G_2/G_1)$ et $p(G_2/P_1)$.
░░b) Construire un arbre pondérée qui exprime les deux premières parties et calculer $p(G_2)$
░░c) Justifier l'égalité $p_n+q_n=1$.
░░d) Démontrer que pour tout entier naturel non nul n; $p_{n+1}=0,5p_n+0,2$
2) Etude de la suite $(p_n)$
On pose pour tout entier naturel n non nul, $v_n=p_n-0,4$
░░a) Prouver que $(v_n)$ est une suite géométrique et exprimer $v_n$ en fonction de n.
░░b) En déduire $p_n$ en fonction de n et déterminer $\lim\limits_{n \to +\infty}{p_n}$.
Solutions ✍
1) a) D'après l'énoncé on a : $p_1=p(G_1)=0,5$ ; $p(G_2/G_1)=0,7$ et $p(G_2/P_1)=1-0,8=0,2$
░░b)
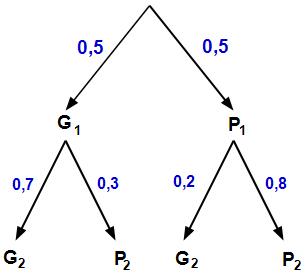 $p(G_2)=p(G_2 \cap G_1)+p(G_2 \cap P_1)$ $=p(G_1) \times p(G_2/G_1)+p(P_1) \times p(G_2/P_1)$ $=0,5 \times 0,7+0,5 \times 0,2=0,45$
$p(G_2)=p(G_2 \cap G_1)+p(G_2 \cap P_1)$ $=p(G_1) \times p(G_2/G_1)+p(P_1) \times p(G_2/P_1)$ $=0,5 \times 0,7+0,5 \times 0,2=0,45$
░░c) Dans chaque partie du jeu, l'un des deux joueurs va gagner la partie c-à-d Pierre gagne ou perd la partie (il n y a pas de match nul) donc les événements $G_n \ et \ P_n$ forment une partition de l'univers et par la suite $p_n+q_n=1$
░░d) Les événements $G_n \ et \ P_n$ forment une partition de l'univers donc d'après la formule des probabilités totales on peut écrire $p(G_{n+1})= p(G_{n+1}\cap G_n)+p(G_{n+1}\cap P_n)$ $=p(G_n) \times p(G_{n+1}/G_n)$ $+p(P_n) \times p(G_{n+1}/P_n)$ $=0,7 \times p_n+q_n \times 0,2$ $=0,7 \times p_n+(1-p_n) \times 0,2$ $=0,5p_n+0,2$
2) a) $v_{n+1}=p_{n+1}-0,4$ $=(0,5p_n+0,2)-0,4$ $=0,5(v_n+0,4)-0,2$ $=0,5v_n$
donc $(v_n)$ est une suite géométrique de raison 0,5.
$ \forall n \in {\Bbb N}^{*},\ v_n$ $=v_1(0,5)^{n-1}$ $=(p_1-0,4)(0,5)^{n-1}$ $=0,1 \times (0,5)^{n-1}$
░░ b) $v_n=p_n-0,4$ $\Longleftrightarrow p_n=v_n+0,4$ $=0,1 \times (0,5)^{n-1}+0,4$
$\lim\limits_{n \to +\infty}{(0,5)}^{n-1}=0$ car $0,5 \in \left]{-1,1}\right[$ d'où $\lim\limits_{n \to +\infty}p_n=0,4$
░░b)

░░c) Dans chaque partie du jeu, l'un des deux joueurs va gagner la partie c-à-d Pierre gagne ou perd la partie (il n y a pas de match nul) donc les événements $G_n \ et \ P_n$ forment une partition de l'univers et par la suite $p_n+q_n=1$
░░d) Les événements $G_n \ et \ P_n$ forment une partition de l'univers donc d'après la formule des probabilités totales on peut écrire $p(G_{n+1})= p(G_{n+1}\cap G_n)+p(G_{n+1}\cap P_n)$ $=p(G_n) \times p(G_{n+1}/G_n)$ $+p(P_n) \times p(G_{n+1}/P_n)$ $=0,7 \times p_n+q_n \times 0,2$ $=0,7 \times p_n+(1-p_n) \times 0,2$ $=0,5p_n+0,2$
2) a) $v_{n+1}=p_{n+1}-0,4$ $=(0,5p_n+0,2)-0,4$ $=0,5(v_n+0,4)-0,2$ $=0,5v_n$
donc $(v_n)$ est une suite géométrique de raison 0,5.
$ \forall n \in {\Bbb N}^{*},\ v_n$ $=v_1(0,5)^{n-1}$ $=(p_1-0,4)(0,5)^{n-1}$ $=0,1 \times (0,5)^{n-1}$
░░ b) $v_n=p_n-0,4$ $\Longleftrightarrow p_n=v_n+0,4$ $=0,1 \times (0,5)^{n-1}+0,4$
$\lim\limits_{n \to +\infty}{(0,5)}^{n-1}=0$ car $0,5 \in \left]{-1,1}\right[$ d'où $\lim\limits_{n \to +\infty}p_n=0,4$
⚜
III. Événements indépendants
Définition
On dit que A et B sont indépendants si, et seulement si, $p(A \cap B)=p(A) \times p(B)$
Remarques
1) Attention à ne pas confondre indépendant et incompatible (qui est synonyme de disjoint c’est-à-dire que $A \cap B=∅$ et non pas $p(A \cap B)=p(A) \times p(B)$).2) Si $p(A) ≠ 0$ (ou $p(B) ≠ 0$) alors A et B sont indépendants si, et seulement si, $p(B/A) = p(B)$ (ou $p(A/B) = p(A)$).
$p(B/A)=p(B)$ traduit le fait que savoir que A est réalisé ne modifie pas la probabilité de B, autrement dit, que la réalisation de A n’a pas d’influence sur la réalisation de B.
Exemple 7
Dans la population, il y a 71% de porteurs de lunettes parmi lesquels 37% ont 55 ans ou plus. Dans la population, il y a 63% de personnes de moins de 55 ans.
On tire au sort une personne dans la population et on considère les deux évènements :
A : « la personne a 55 ans ou plus ».
L : « la personne porte des lunettes ».
Les évènements A et L sont-ils indépendants ?
On tire au sort une personne dans la population et on considère les deux évènements :
A : « la personne a 55 ans ou plus ».
L : « la personne porte des lunettes ».
Les évènements A et L sont-ils indépendants ?
Solutions ✍
D’après l’énoncé, $p(L) = 0,71$ ; $p(A) = 1 − 0,63 = 0,37$ et $p(A/L)=0,37$
Donc $p(A) \times p(L)=0,37 \times 0,71 = 0,2627$ et $p(A\cap L)=p(L)\times p(A/L)$ $=0,71 × 0,37 = 0,2627$
On a : $p(A) \times p(L)=p(A\cap L)$ donc les événements A et L sont indépendants.
Donc $p(A) \times p(L)=0,37 \times 0,71 = 0,2627$ et $p(A\cap L)=p(L)\times p(A/L)$ $=0,71 × 0,37 = 0,2627$
On a : $p(A) \times p(L)=p(A\cap L)$ donc les événements A et L sont indépendants.
Exemple 8
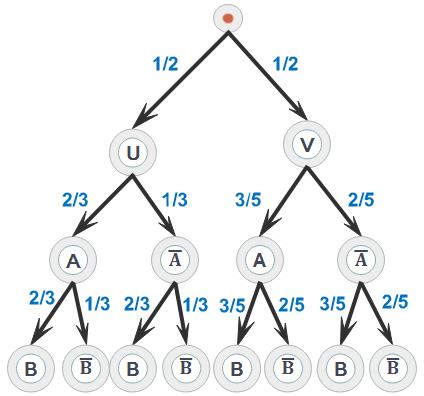
Une urne U contient trois boules noires et six boules vertes.
Une urne V contient deux boules noires et trois boules vertes.
On choisit une urne au hasard et on tire successivement deux boules, en remettant chaque fois la boule, dans l’urne choisie.
On considère les événements : A « obtenir une boule verte au premier tirage » et B « obtenir une boule verte au deuxième tirage ».
Les événements A et B sont-ils indépendants ?
Une urne V contient deux boules noires et trois boules vertes.
On choisit une urne au hasard et on tire successivement deux boules, en remettant chaque fois la boule, dans l’urne choisie.
On considère les événements : A « obtenir une boule verte au premier tirage » et B « obtenir une boule verte au deuxième tirage ».
Les événements A et B sont-ils indépendants ?
Solutions ✍
Considérons les événements U « le tirage se fait dans l'urne U » et V « le tirage se fait dans l'urne V »
On peut résumer la situation à l'aide d'un arbre pondérée
 En utilisant l'arbre pondérée on a:
En utilisant l'arbre pondérée on a:
$p(A)=p(U)\times p(A/U)$ $+p(V)\times p(A/V)$ $=\frac{1}{2}\times \frac{6}{9}+\frac{1}{2}\times \frac{3}{5}$ $=\frac{1}{3}+ \frac{3}{10}=\frac{19}{30}$
Sachant que la probabilité d'un événement est la somme des probabilités des chemins conduisant à cet événement et que la probabilité d'un chemin est le produit des probabilités des branches de ce chemin, on peut alors écrire:
$p(B)=\frac{1}{2} \frac{2}{3} \frac{2}{3}+ \frac{1}{2} \frac{1}{3} \frac{2}{3} $ $+\frac{1}{2} \frac{3}{5} \frac{3}{5}+\frac{1}{2} \frac{2}{5} \frac{3}{5}$ $=\frac{2}{9}+\frac{1}{9}+\frac{9}{50}+\frac{6}{50}$ $=\frac{3}{9}+\frac{15}{50}=\frac{1}{3}+\frac{3}{10}$ $=\frac{19}{30}$
$p(A\cap B)$ :« Les deux boules tirées sont vertes »
Les chemins à suivre sur l'arbre pondérée pour que cet événement soit réalisé sont: $\bullet \to U \to A \to B$ ou $\bullet \to V \to A \to B$ donc
$p(A\cap B)=\frac{1}{2}{\left({\frac{2}{3}}\right)}^{2}+\frac{1}{2}{\left({\frac{3}{5}}\right)}^{2}=\frac{362}{900}$ et on a: $p(A)\times p(B)={\left({\frac{19}{30}}\right)}^2=\frac{361}{900}$
$p(A\cap B) \ne p(A)\times p(B)$ donc A et B ne sont pas indépendants.
On peut résumer la situation à l'aide d'un arbre pondérée

$p(A)=p(U)\times p(A/U)$ $+p(V)\times p(A/V)$ $=\frac{1}{2}\times \frac{6}{9}+\frac{1}{2}\times \frac{3}{5}$ $=\frac{1}{3}+ \frac{3}{10}=\frac{19}{30}$
Sachant que la probabilité d'un événement est la somme des probabilités des chemins conduisant à cet événement et que la probabilité d'un chemin est le produit des probabilités des branches de ce chemin, on peut alors écrire:
$p(B)=\frac{1}{2} \frac{2}{3} \frac{2}{3}+ \frac{1}{2} \frac{1}{3} \frac{2}{3} $ $+\frac{1}{2} \frac{3}{5} \frac{3}{5}+\frac{1}{2} \frac{2}{5} \frac{3}{5}$ $=\frac{2}{9}+\frac{1}{9}+\frac{9}{50}+\frac{6}{50}$ $=\frac{3}{9}+\frac{15}{50}=\frac{1}{3}+\frac{3}{10}$ $=\frac{19}{30}$
$p(A\cap B)$ :« Les deux boules tirées sont vertes »
Les chemins à suivre sur l'arbre pondérée pour que cet événement soit réalisé sont: $\bullet \to U \to A \to B$ ou $\bullet \to V \to A \to B$ donc
$p(A\cap B)=\frac{1}{2}{\left({\frac{2}{3}}\right)}^{2}+\frac{1}{2}{\left({\frac{3}{5}}\right)}^{2}=\frac{362}{900}$ et on a: $p(A)\times p(B)={\left({\frac{19}{30}}\right)}^2=\frac{361}{900}$
$p(A\cap B) \ne p(A)\times p(B)$ donc A et B ne sont pas indépendants.
Autres articles
Fonction logarithme népérien
Etude de fonctions
Cryptographie
Probabilité conditionnelle
Identité de Bezout
Divisibilité dans ℤ
Le triangle de Pascal
Les nombres de Mersenne
Théorie des situations
Evaluation du travail de l'élève
Les théories de l'apprentissage
Eléments de logique mathématiques
Fractales (Partie I) - Arbres fractales
Fractales (Partie II) - Plantes fractales
Fractales (Partie III) - Courbes et formes fractales
Fractales (Partie IV) - Ensemble de Mandelbrot
MathJax - Beautiful math in all browsers
Dénombrement
Droite dans le plan
Etude de fonctions
Cryptographie
Probabilité conditionnelle
Identité de Bezout
Divisibilité dans ℤ
Le triangle de Pascal
Les nombres de Mersenne
Théorie des situations
Evaluation du travail de l'élève
Les théories de l'apprentissage
Eléments de logique mathématiques
Fractales (Partie I) - Arbres fractales
Fractales (Partie II) - Plantes fractales
Fractales (Partie III) - Courbes et formes fractales
Fractales (Partie IV) - Ensemble de Mandelbrot
MathJax - Beautiful math in all browsers
Dénombrement
Droite dans le plan
Malek Bellasfar05-05-2021 21:08:11
on veut plus
Connectez vous pour ajouter des commentaires.
Commentaires