Courbes et formes fractales
Créé par Dhaouadi Nejib 2018
Les courbes fractales sont les fractales les plus simples à se représenter, elles sont obtenues grâce à une construction géométrique.
Ce sont des courbes continues qui n'ont aucune tangente en tous ses points. la dimension est différente de 1 et comprise entre 1 et 2.
Ce sont des courbes continues qui n'ont aucune tangente en tous ses points. la dimension est différente de 1 et comprise entre 1 et 2.
Exemple 1 (Courbe de Von Koch )
Le flocon de Koch est l'une des premières courbes fractales à avoir été décrites (bien avant l'invention du terme « fractal(e) »).
Elle a été inventée en 1904 par le mathématicien suédois Helge von Koch.
Elle a été inventée en 1904 par le mathématicien suédois Helge von Koch.
On peut la créer à partir d'un segment de droite, en modifiant récursivement chaque segment de la façon suivante :
Construction à l'aide du L-system:
Axiome: F++F++F
Règle : F--> F-F++F-F
Angle : 90°
- Diviser le segment de droite en trois segments de longueurs égales.
- Construire un triangle équilatéral ayant pour base le segment médian de la première étape.
- Supprimer le segment qui était la base du triangle de la deuxième étape.
- Répétez cette opération sur la figure obtenue; Et, ceci, autant de fois que vous le voulez.
Construction à l'aide du L-system:
Axiome: F++F++F
Règle : F--> F-F++F-F
Angle : 90°
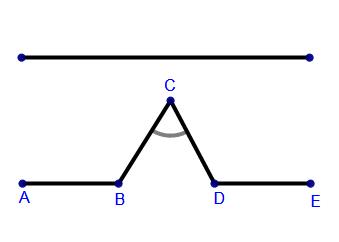
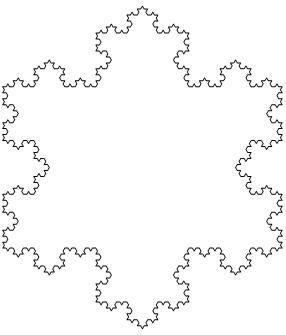
Chaque segment donne naissance à 4 petits segments et 3 fois la longueur d'un petit segment est égale à la longueur du segment parent.
Donc la dimension de la courbe de koch est égale à : $\frac{ln4}{ln3}\simeq 1,261$
Donc la dimension de la courbe de koch est égale à : $\frac{ln4}{ln3}\simeq 1,261$
La longueur de la courbe de koch
Supposons que le triangle de départ est de coté p. Chaque segment est remplacé par 4 petits segments isométriques, alors la longueur de la courbe après n étérations est une suite géométrique de raison 4/3 et de premier tèrme 3p. Donc la logueur du flocon de koch est égale à : $3p\left({\frac{4}{3}}\right)^n $
Alors si n tend vers $+\infty$, la longueur de cette courbe tend vers $+\infty$
Alors si n tend vers $+\infty$, la longueur de cette courbe tend vers $+\infty$
L'aire du flocon de koch
Si on a choisi l'unité d'aire de telle sorte que le triangle construit à la première itération soit d'aire 1, alors l'aire de chacun des quatre triangles construits lors de la seconde itération est 1/9 : on a donc augmenté l'aire totale de 4/9. Pour l'itération n, on ajoute $ 4^{{n-1}}\times \left({\frac {1}{9}}\right)^{{n-1}}$. La surface totale s'obtient finalement en sommant une série géométrique :
$ \sum _{{n=0}}^{\infty }\left({4 \over 9}\right)^{n}={1 \over 1-4/9}={9 \over 5}$
Exemple 2 (Le triangle de Sierpinski)
Le triangle de Sierpinski (appelé aussi fanion de Sierpinski) est une fractale qu'on peut la construire de la façon suivante :
On part d'un triangle équilatéral auquel on ôte le triangle construit à partir du milieu des 3 côtés.
on obtient alors 3 nouveaux triangles auxquels on réapplique le même procédure.
on répète cette construction plusieurs fois (ça dépend de la capacité de votre ordinateur).
Paramètres L-system
Axiome:F-G-G-G
Règles:
F --> F-G+F+G-F
G --> GG
Angle : 60°
Règles:
F --> F-G+F+G-F
G --> GG
Angle : 60°
Il est facile à remarquer que l'aire du domaine obtenu après n itération est égale à $\left({\frac{3}{4}}\right)^{n}a_0$ où $a_0$ est l'aire du triangle initial.
Le nombre de triangles à traiter (en noir) après n itérations est égal à $3^n$.
Le nombre de triangles à traiter (en noir) après n itérations est égal à $3^n$.
Exemple 3 (Courbe de Peano)
Courbe de Peano (wikipedia)
Une courbe de Peano est une courbe plane paramétrée par une fonction continue sur l'intervalle unité $[0, 1]$, surjective dans le carré $[0, 1]×[0, 1]$, c'est-à-dire que la courbe passe par chaque point du carré : elle « remplit l'espace ». Toutes ces courbes sont des fractales : bien que formées d'une simple ligne, elles sont de dimension 2. Ce type de courbes est nommé en l'honneur de Giuseppe Peano, qui fut le premier à en décrire une.
Dans un article de 18901 Giuseppe Peano décrit une courbe auto-intersectante qui passe par tous les points de la surface du carré unité. En construisant une surjection de l'intervalle réel unité vers le carré unité du plan, il illustre un résultat de Georg Cantor qui, en 1877, avait établi que le carré a la puissance du continu, c'est-à-dire le même cardinal que l'intervalle. La nouveauté est que la surjection construite par Peano est continue.
La clé passe par l'élaboration d'une courbe nulle part différentiable. Toutes les courbes rencontrées jusqu'alors étaient différentiables par parties (elles avaient une dérivée continue sur chaque intervalle). En 1872, Karl Weierstrass avait bien décrit une fonction qui était continue en tout point mais différentiable en aucun point. Mais aucune de ces courbes ne pouvait remplir le carré unité. La courbe de Peano, à la fois nulle part différentiable et remplissant le plan, était donc fortement contre-intuitive.
Paramètres L-system
Axiome : L
Règles :
L ---> LFRFL-F-RFLFR+F+LFRFL
R ---> LFRFL-F-RFLFR+F+LFRFL
Angle : 90°
Dans un article de 18901 Giuseppe Peano décrit une courbe auto-intersectante qui passe par tous les points de la surface du carré unité. En construisant une surjection de l'intervalle réel unité vers le carré unité du plan, il illustre un résultat de Georg Cantor qui, en 1877, avait établi que le carré a la puissance du continu, c'est-à-dire le même cardinal que l'intervalle. La nouveauté est que la surjection construite par Peano est continue.
La clé passe par l'élaboration d'une courbe nulle part différentiable. Toutes les courbes rencontrées jusqu'alors étaient différentiables par parties (elles avaient une dérivée continue sur chaque intervalle). En 1872, Karl Weierstrass avait bien décrit une fonction qui était continue en tout point mais différentiable en aucun point. Mais aucune de ces courbes ne pouvait remplir le carré unité. La courbe de Peano, à la fois nulle part différentiable et remplissant le plan, était donc fortement contre-intuitive.
Paramètres L-system
Axiome : L
Règles :
L ---> LFRFL-F-RFLFR+F+LFRFL
R ---> LFRFL-F-RFLFR+F+LFRFL
Angle : 90°
Exemple 4 (Courbe de Hilbert)
Courbe de Hilbert
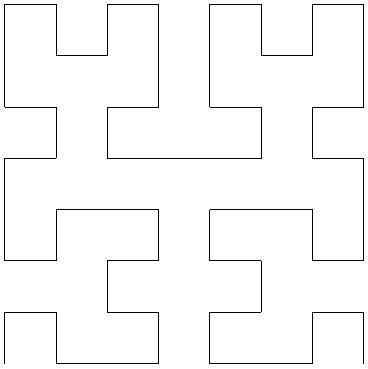
La courbe de Hilbert est une courbe continue remplissant un carré. Elle a été décrite pour la première fois par le mathématicien allemand David Hilbert en 1891.
Comme elle couvre un carré, sa dimension de Hausdorff et sa dimension topologique sont égales à 2. On la considère cependant comme faisant partie des fractales.
La longueur euclidienne de $H_n$ (la courbe continue obtenue à la n-ième itération) est ${\displaystyle 2^{n}-{1 \over 2^{n}}}$. (wikipedia)
Comme elle couvre un carré, sa dimension de Hausdorff et sa dimension topologique sont égales à 2. On la considère cependant comme faisant partie des fractales.
La longueur euclidienne de $H_n$ (la courbe continue obtenue à la n-ième itération) est ${\displaystyle 2^{n}-{1 \over 2^{n}}}$. (wikipedia)
Paramètres L-system
Axiome: L
Règles :
L ---> –RF+LFL+FR−
R ---> +LF−RFR−FL+
Angle = 90°
Axiome: L
Règles :
L ---> –RF+LFL+FR−
R ---> +LF−RFR−FL+
Angle = 90°
Exemple 5 (Courbe de Gosper)
Courbe de Gosper
En géométrie, la courbe de Gosper, découverte par Bill Gosper en 1973, et popularisée par Martin Gardner en 1976, est une courbe de Peano remplissant le plan. Il s'agit d'une courbe fractale, voisine, dans sa construction, de la courbe du dragon ou de la courbe de Hilbert
La courbe de Gosper est obtenue par un processus itératif consistant à remplacer, à chaque itération, chaque segment par 7 segments d'une longueur réduite de $1/\sqrt{7}$.
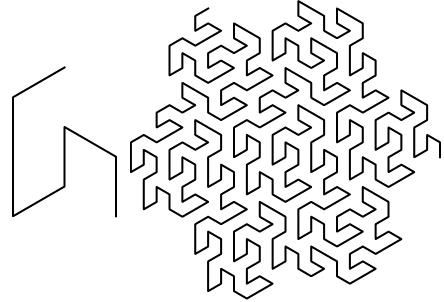La courbe ayant ainsi 7 similitudes internes de rapport $1/\sqrt{7}$, sa dimension fractale tend vers 2, elle pave donc le plan. À l'infini, l'ensemble rempli par la courbe est appelé île de Gosper.
Les paramètres L-system
Axiome : F
Règles :
F ---> F-G--G+F++FF+G-
G ---> +F-GG--G-F++F+G
Angle : 60°
La courbe de Gosper est obtenue par un processus itératif consistant à remplacer, à chaque itération, chaque segment par 7 segments d'une longueur réduite de $1/\sqrt{7}$.
Les paramètres L-system
Axiome : F
Règles :
F ---> F-G--G+F++FF+G-
G ---> +F-GG--G-F++F+G
Angle : 60°
Autres fractales
Quadratique de Gosper
L-system
Axiome : YF
Règles :
X --> XFX-YF-YF+FX+FX-YF-YFFX+YF+FXFXYF
-FX+YF+FXFX+YF-FXYF-YF-FX+FX+YFYF-
Y ---> +FXFX-YF-YF+FX+FXYF+FX-YFYF-FX-YF
+FXYFYF-FX-YFFX+FX+YF-YF-FX+FX+YFY
Angle = 90°
Iterations = 2
Courbe de Sierpiński
L-System code Axiome : R-F-R-F-R-F-R Règles : L ---> +R-F-R+ R ---> -L+F+L- Angle = 45° Iterations = 10
Tapis de Sierpiński
L-System code Axiome : F Règles : F ---> F+F-F-F-G+F+F+F-F G ---> GGG Angle = 90° Iterations = 6
Courbe du dragon
L-System code Axiome : FX Règles : X ---> X+YF Y ---> FX-Y Angle = 90° Iterations = 11
Triangles
L-System code Axiome : F+F+F Règle : F ---> F-F+F Angle = 120° Iterations = 7
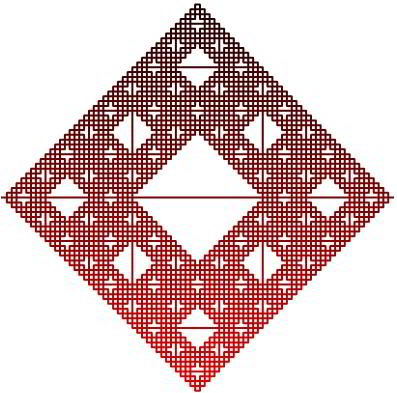
Square Sierpinski
L-System code Axiome : F+XF+F+XF Règle : X ---> XF-F+F-XF+F+XF-F+F-X Angle = 90° Iterations = 5
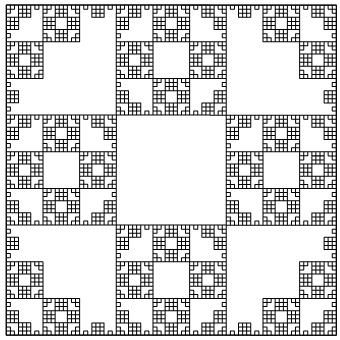
Plaque
L-System code Axiome : F+F+F+F Règle : F ---> FF+F+F+F+FF Angle = 90° Iterations = 5
Autres articles
Fonction logarithme népérien
Etude de fonctions
Cryptographie
Probabilité conditionnelle
Identité de Bezout
Divisibilité dans ℤ
Le triangle de Pascal
Les nombres de Mersenne
Théorie des situations
Evaluation du travail de l'élève
Les théories de l'apprentissage
Eléments de logique mathématiques
Fractales (Partie I) - Arbres fractales
Fractales (Partie II) - Plantes fractales
Fractales (Partie III) - Courbes et formes fractales
Fractales (Partie IV) - Ensemble de Mandelbrot
MathJax - Beautiful math in all browsers
Dénombrement
Droite dans le plan
Etude de fonctions
Cryptographie
Probabilité conditionnelle
Identité de Bezout
Divisibilité dans ℤ
Le triangle de Pascal
Les nombres de Mersenne
Théorie des situations
Evaluation du travail de l'élève
Les théories de l'apprentissage
Eléments de logique mathématiques
Fractales (Partie I) - Arbres fractales
Fractales (Partie II) - Plantes fractales
Fractales (Partie III) - Courbes et formes fractales
Fractales (Partie IV) - Ensemble de Mandelbrot
MathJax - Beautiful math in all browsers
Dénombrement
Droite dans le plan
Connectez vous pour ajouter des commentaires.