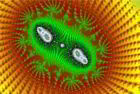
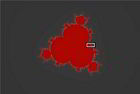
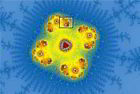
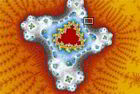
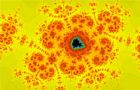
Ensemble de Mandelbrot
Dhaouadi Nejib

Mandelbrot mit ainsi en avant la géométrie fractale, une nouvelle forme de pensée dans les domaines des mathématiques et des sciences naturelles. Il a conçu des méthodes d'observation basées sur l'autosimilarité. Mandelbrot montra que de nombreuses structures naturelles apparemment très complexes présentent en réalité une régularité géométrique invariante à différentes échelles. Il publia "The Fractal geometry of Nature" en 1982.
Une fractale est le produit final obtenu par la répétition infinie d'un processus géométrique bien défini. Quel que soit le niveau d'observation, on constate qu'il existe un modèle qui se répète sans que l'échelle d'observation ait une quelconque importance.
Le procédé est généralement très simple. En raison de l'itération infinie, on obtient des structures d'une complexité extraordinaire.
En mathématiques, l'ensemble de Mandelbrot est une fractale définie comme l'ensemble des points c du plan complexe pour lesquels la suite de nombres complexes définie par récurrence par : $$\begin{cases}z_{0}=0\\z_{n+1}=z_{n}^{2}+c\end{cases}$$ est bornée.
Pour définir mathématiquement la fractale de Mandelbrot on associe à chaque point du plan complexe, la suite $z_{n+1}=z_n^2+c$ avec $z_0=0$ et c=a+ib l'affixe du point. Tous les points pour lesquels la suite est bornée vont constituer l'ensemble de Mandelbrot.
On demontre mathématiquement que si le module de $z_n$ est supérieur à 2 la suite diverge et on déduit que l'ensemble de Mandelbrot est forcément inclus dans le cercle de rayon 2 et de centre (0,0).
L'ensemble de Mandelbrot est devenu populaire hors des mathématiques, comme inspiration artistique et comme exemple de structure complexe venant de l'application de règles simples. C'est l'un des exemples les plus connus de visualisation mathématique.
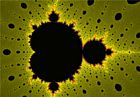
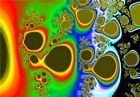
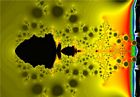
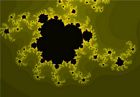
Représentations graphiques des fractales de Mandelbrot
Avec $z_n=x_n+iy_n$ on trouve les relations de récurrence sur les suites réelles :$$
x_{n+1}=x_n^2-y_n^2+a \\
y_{n+1}=2 x_n y_n+b
$$
Pour déterminer si un point $M(a,b)$ de la rectangle de traçage appartient à l'ensemble de Mandelbrot on bouclera sur la suite complexe jusqu'à ce qu'elle diverge ce qui est acquis si $|z_n|^2= x_n^2+y_n^2>4$ ou que le nombre de boucles soit supérieur à une limite maxIterations fixée.
Images de la fractale : $z_{n+1}=z_n^2+c$
Images de la fractale : $z_{n+1}=z_n^3+c$
Images de la fractale : $z_{n+1}=z_n^4+c$
Belles images de fractales diverses
Autres articles
Fonction logarithme népérien
Etude de fonctions
Cryptographie
Probabilité conditionnelle
Identité de Bezout
Divisibilité dans ℤ
Le triangle de Pascal
Les nombres de Mersenne
Théorie des situations
Evaluation du travail de l'élève
Les théories de l'apprentissage
Eléments de logique mathématiques
Fractales (Partie I) - Arbres fractales
Fractales (Partie II) - Plantes fractales
Fractales (Partie III) - Courbes et formes fractales
Fractales (Partie IV) - Ensemble de Mandelbrot
MathJax - Beautiful math in all browsers
Dénombrement
Droite dans le plan
Etude de fonctions
Cryptographie
Probabilité conditionnelle
Identité de Bezout
Divisibilité dans ℤ
Le triangle de Pascal
Les nombres de Mersenne
Théorie des situations
Evaluation du travail de l'élève
Les théories de l'apprentissage
Eléments de logique mathématiques
Fractales (Partie I) - Arbres fractales
Fractales (Partie II) - Plantes fractales
Fractales (Partie III) - Courbes et formes fractales
Fractales (Partie IV) - Ensemble de Mandelbrot
MathJax - Beautiful math in all browsers
Dénombrement
Droite dans le plan
Connectez vous pour ajouter des commentaires.