La droite dans le plan
Créé par Dhaouadi Nejib
I. Introduction
Pour commencer, nous rappelons les axiomes d'Euclide concernant la droite dans le plan:
Dans cet article, on va citer la plupart des méthodes connues pour déterminer une équation cartésienne d'une droite ou une représentation paramètrique.
On suppose dans la suite que le plan est rapporté à un repère cartésien $(0,\vec i, \vec j)$
- il existe toujours une seule droite qui passe par deux points distincts du plan.
- tout segment peut être étendu suivant sa direction en une droite (infinie).
- étant donné un point et une droite ne passant pas par ce point, il existe une seule droite passant par ce point et parallèle à la première.
Dans cet article, on va citer la plupart des méthodes connues pour déterminer une équation cartésienne d'une droite ou une représentation paramètrique.
On suppose dans la suite que le plan est rapporté à un repère cartésien $(0,\vec i, \vec j)$
II. Pente d'une droite
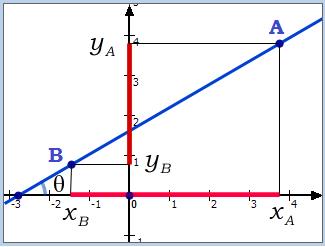
Soient $A(x_A,y_A)$ et $B(x_B,y_B)$ deux points distincts d'une droite D.
Si cette droite n'est pas parallèle à l'axe des ordonnées (c-à-d $x_A\neq x_B$) alors elle admet une pente définie par: $$ m=\frac{y_B-y_A}{x_B-x_A}$$ On a aussi $m=tan \theta$ où $\theta$ est la mesure en radian de l'angle que fait la droite avec l'axe des abscisses.
Si cette droite n'est pas parallèle à l'axe des ordonnées (c-à-d $x_A\neq x_B$) alors elle admet une pente définie par: $$ m=\frac{y_B-y_A}{x_B-x_A}$$ On a aussi $m=tan \theta$ où $\theta$ est la mesure en radian de l'angle que fait la droite avec l'axe des abscisses.
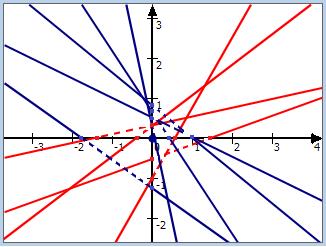
Le signe de la pente m d'une droite D dépend des positions de cette droite par rapport aux quatre-quarts du plan définis par le repère choisi.(Voir la figure)
Les pentes des droites tracées en rouge sont positives
Les pentes des droites tracées en bleu sont négatives
⚠ Une droite parallèle à l'axe des ordonnées n'a pas de pente.
✍ Une droite parallèle à l'axe des abscisses sa pente est nulle.
Les pentes des droites tracées en rouge sont positives
Les pentes des droites tracées en bleu sont négatives
⚠ Une droite parallèle à l'axe des ordonnées n'a pas de pente.
✍ Une droite parallèle à l'axe des abscisses sa pente est nulle.
III. Equation cartésienne d'une droite
1. Droite définie à l'aide de deux points distincts
On donne une droite D passant par deux points $A(x_A,y_A)$ et $B(x_B,y_B)$ et on se propose de déterminer une équation cartésienne de cette droite.
Premier cas: $\style{color: blue} {x_A = x_B}$
Dans ce cas la droite D est parallèle à l'axe des ordonnées et une équation cartésienne de cette droite est : $\boxed{x=x_A}$
deuxième cas: $\style{color: blue} {x_A \neq x_B}$
$M(x,y) \in D \iff \overrightarrow{AM}$ et $ \overrightarrow{AB}$ sont colinéaires $\iff \left|{\begin{matrix}{x-x_A}&{x_B-x_A}\\{y-y_A}&{y_B-y_A}\end{matrix}}\right|=0 \iff (x-x_A)(y_B-y_A)-(y-y_A)(x_B-x_A)=0$
Finalement l'équation cartésienne de la droite D est: $\boxed{y=\frac{y_B-y_A}{x_B-x_A}(x-x_A)+y_A} (1)$
Autrement
On sait que la droite D admet pour équation cartésienne $y=ax+b$ où a et b sont des réels.
Et puisque la droite D passe par les points A et B alors on obtient le système suivant a deux inconnues a et b. $ \left\{{\begin{aligned}&{y_A=ax_A+b}\\&{y_B=ax_B+b}\end{aligned}}\right.$
Par soustraction des deux équations on obtient $(y_B-y_A)=a(x_B-x_A)$ ou encore $a=\frac{y_B-y_A}{x_B-x_A}$ et puis $b=y_A-ax_A=y_A-\frac{y_B-y_A}{x_B-x_A}x_A$
En remplaçant a et b par leurs valeurs on retrouve la formule $(1)$
Premier cas: $\style{color: blue} {x_A = x_B}$
Dans ce cas la droite D est parallèle à l'axe des ordonnées et une équation cartésienne de cette droite est : $\boxed{x=x_A}$
deuxième cas: $\style{color: blue} {x_A \neq x_B}$
$M(x,y) \in D \iff \overrightarrow{AM}$ et $ \overrightarrow{AB}$ sont colinéaires $\iff \left|{\begin{matrix}{x-x_A}&{x_B-x_A}\\{y-y_A}&{y_B-y_A}\end{matrix}}\right|=0 \iff (x-x_A)(y_B-y_A)-(y-y_A)(x_B-x_A)=0$
Finalement l'équation cartésienne de la droite D est: $\boxed{y=\frac{y_B-y_A}{x_B-x_A}(x-x_A)+y_A} (1)$
Autrement
On sait que la droite D admet pour équation cartésienne $y=ax+b$ où a et b sont des réels.
Et puisque la droite D passe par les points A et B alors on obtient le système suivant a deux inconnues a et b. $ \left\{{\begin{aligned}&{y_A=ax_A+b}\\&{y_B=ax_B+b}\end{aligned}}\right.$
Par soustraction des deux équations on obtient $(y_B-y_A)=a(x_B-x_A)$ ou encore $a=\frac{y_B-y_A}{x_B-x_A}$ et puis $b=y_A-ax_A=y_A-\frac{y_B-y_A}{x_B-x_A}x_A$
En remplaçant a et b par leurs valeurs on retrouve la formule $(1)$
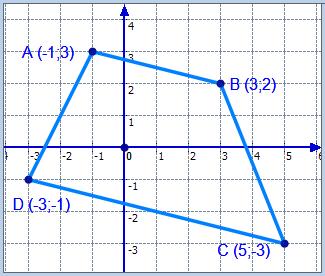
Exercice 1
Considérons un trapèze ABCD où $A(-1,3),B(3,2),C(5,-3)$ et $D(-3,-1)$. On pose $I=(AC)\cap(BD)$
Donner une équation cartésienne de chacune des droites (AC) et (BD) et puis déduire les coordonnées du point I.
Donner une équation cartésienne de chacune des droites (AC) et (BD) et puis déduire les coordonnées du point I.
$\require{action.js}\toggle
{\text{Cliquer ici pour voir la solution}}
{\begin{aligned}&{\hand(AC): x+y-2=0}\\
&{\hand (BD):x-2y+1=0}\\
&{\hand I(1,1)}\end{aligned}}
\endtoggle$
2. Droite définie à l'aide d'un point et un vecteur directeur
✍
Soit D est une droite définie par la donné d'un point $A(x_A,y_A)$ et un vecteur directeur $\vec u \left({\begin{aligned}&{a}\\&{b}\end{aligned}}\right)$.
$M(x,y) \in D \iff \overrightarrow{AM}$ et $ \overrightarrow{u}$ sont colinéaires $\iff \left|{\begin{matrix}{x-x_A}&{a}\\{y-y_A}&{b}\end{matrix}}\right|=0 \iff b(x-x_A)-a(y-y_A)=0$
Finalement l'équation cartésienne de la droite D est: $\boxed{b(x-x_A)-a(y-y_A)=0}$
Autrement
Si $a \neq 0$ alors la pente de la droite D est le réel $m=\frac ba$ et par suite une équation de D est de la forme $y=\frac{b}{a}x+c$ et puisque A$\in$ D alors $y_A=\frac{b}{a}x_A+c \iff c=y_A-\frac{b}{a}x_A$
Finalement l'équation cartésienne de la droite D est: $\boxed{y=\frac{b}{a}(x-x_A)+y_A}$
$M(x,y) \in D \iff \overrightarrow{AM}$ et $ \overrightarrow{u}$ sont colinéaires $\iff \left|{\begin{matrix}{x-x_A}&{a}\\{y-y_A}&{b}\end{matrix}}\right|=0 \iff b(x-x_A)-a(y-y_A)=0$
Finalement l'équation cartésienne de la droite D est: $\boxed{b(x-x_A)-a(y-y_A)=0}$
Autrement
Si $a \neq 0$ alors la pente de la droite D est le réel $m=\frac ba$ et par suite une équation de D est de la forme $y=\frac{b}{a}x+c$ et puisque A$\in$ D alors $y_A=\frac{b}{a}x_A+c \iff c=y_A-\frac{b}{a}x_A$
Finalement l'équation cartésienne de la droite D est: $\boxed{y=\frac{b}{a}(x-x_A)+y_A}$
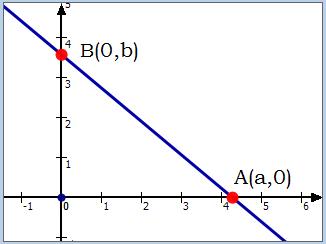
3. Droite définie à l'aide de ses points d'intersection avec les axes
Soit D une droite définie par la donnée des deux points distincts $A(a,0)$ et $B(0,b)$
Si $a=0$ alors une équation de D est: $x=0$
Si $b=0$ alors une équation de D est: $y=0$
Si $a \neq 0 \; et \; b\neq 0$ alors une équation de D est : $\boxed{\frac {x} {a} + \frac {y}{b}=1}$
Si $a=0$ alors une équation de D est: $x=0$
Si $b=0$ alors une équation de D est: $y=0$
Si $a \neq 0 \; et \; b\neq 0$ alors une équation de D est : $\boxed{\frac {x} {a} + \frac {y}{b}=1}$
4. Droite passant par un point donné et parallèle à une droite donnée.
- Deux droites sont parallèles si et seulement si leurs vecteurs directeurs sont colinéaires.
- Deux droites sont parallèles si et seulement si tout vecteur directeur de l'une est aussi un vecteur directeur de l'autre.
- Deux droites sont parallèles si et seulement si ces deux droites ont la même pente (si elle existe).
Soit $\Delta$ une droite dont une équation cartésienne est : $ax+by+c=0$ où a, b et c sont des réels tels que $(a,b) \neq (0,0)$
Si D est une droite passant par un point $A(x_A,y_A)$ et parallèle à $\Delta$, alors le vecteur $\vec u \left({\begin{aligned}{-b}\\{a}\end{aligned}}\right)$ directeur de $\Delta$ est aussi directeur de D donc la droite D admet une équation cartésienne de la forme $ax+by+c'=0$ et pour déterminer la constante c', il suffit d'écrire $A \in D \iff ax_A+by_A+c'=0 \iff c'=-ax_A-by_A$ et finalement l'équation de D est : $\boxed{a(x-x_A)+b(y-y_A)=0} $
Droites parallèle entre eux et non parallèles à l'axe des ordonnées
Une famille de droites parallèle entre eux et non parallèles à l'axe des ordonnées ont la même pente et ont pour équations cartésiennes de la forme $y=ax+b$ où a est la pente et b l'ordonnée à l'origine.
Dans l'exemple donné (voir l'image), remarquer bien l'ordonnée à l'origine pour chaque droite.
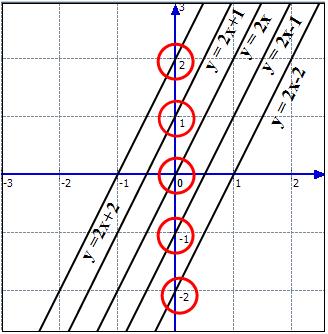
5. Droite définie à l'aide d'un point et un vecteur normal
On suppose ici que le repère $(O,\vec i,\vec j)$ est orthonormé.
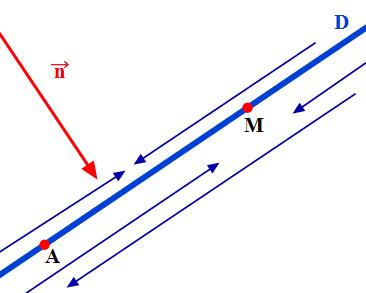✍ Soient $A(x_A,y_A)$ un point du plan et $\vec n \left({\begin{aligned}&{a}\\&{b}\end{aligned}}\right)$ un vecteur non nul.
La droite D passant par A et admettant $\vec n$ comme vecteur normal est l'ensemble des points M du plan tels que $\vec {AM}\centerdot \vec n=0$ $$D=\left\{{M \in P / \vec {AM}\centerdot \vec n=0 }\right\}$$
D'après ce qui précède, une équation cartésienne de D est de la forme $\boxed {a(x-x_A)+b(y-y_A)=0}$
Réciproquement, si une droite D admet une équation cartésienne de la forme $ax+by+c=0$ alors le vecteur $\vec u \left({\begin{aligned}&{a}\\&{b}\end{aligned}}\right)$ est un vecteur normal à cette droite.
⚠ Ces résultats (III. 5.)sont valables seulement dans un repère orthonormé.
✍
$\vec n$ est un vecteur normal à une droite D si et seulement si $\vec n$ est non nul et orthogonal à tout vecteur directeur de D.
La droite D passant par A et admettant $\vec n$ comme vecteur normal est l'ensemble des points M du plan tels que $\vec {AM}\centerdot \vec n=0$ $$D=\left\{{M \in P / \vec {AM}\centerdot \vec n=0 }\right\}$$
D'après ce qui précède, une équation cartésienne de D est de la forme $\boxed {a(x-x_A)+b(y-y_A)=0}$
Réciproquement, si une droite D admet une équation cartésienne de la forme $ax+by+c=0$ alors le vecteur $\vec u \left({\begin{aligned}&{a}\\&{b}\end{aligned}}\right)$ est un vecteur normal à cette droite.
⚠ Ces résultats (III. 5.)sont valables seulement dans un repère orthonormé.
Exercice 2
Dans le plan rapporté à un repère orthonormé $(O,\vec i,\vec j)$ on donne les points $A(-3,4),B(5,0)$ et $C(-4,-3)$
Dans le triangle ABC, on note A' le pied de la hauteur issue de A, B' le pied de la hauteur issue de B et H son orthocentre.
Déterminer les coordonnées des points A',B' et H.
Dans le triangle ABC, on note A' le pied de la hauteur issue de A, B' le pied de la hauteur issue de B et H son orthocentre.
Déterminer les coordonnées des points A',B' et H.
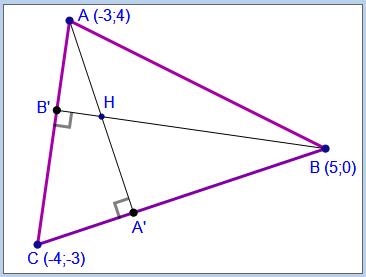
$\require{action.js}\toggle
{\text{Cliquer ici pour voir la solution}}
{\begin{aligned}
&{\hand A'(-1,-2)}\\
&{\hand B'\left({\frac {-17}{5},\frac {6}{5}}\right)} \\
&{\hand H(-2,1)}\end{aligned}}
\endtoggle$
III. Représentation paramétrique d'une droite
1. Représentation paramétrique d'une droite définie à l'aide d'un point et un vecteur directeur
Dans le plan muni du repère cartésien $(O,\vec i,\vec j)$ on considère une droite D passant par un point $A(x_A,y_A)$ et de vecteur directeur $\vec u \left({\begin{aligned}&{a}\\&{b}\end{aligned}}\right)$
$M(x,y) \in D \Longleftrightarrow \; il \; existe \lambda \in \Bbb R \; tq \; \vec {AM}=\lambda \vec u \\ \Longleftrightarrow \left\{{\begin{aligned}&{x-x_A=\lambda a}\\&{y-y_A=\lambda b}\end{aligned}}\right. \Longleftrightarrow \left\{{\begin{aligned}&{x=x_A+\lambda a}\\&{y=y_A+\lambda b}\end{aligned}}\right.$
Ce dernier système forme une représentation paramétrique de la droite D.
$M(x,y) \in D \Longleftrightarrow \; il \; existe \lambda \in \Bbb R \; tq \; \vec {AM}=\lambda \vec u \\ \Longleftrightarrow \left\{{\begin{aligned}&{x-x_A=\lambda a}\\&{y-y_A=\lambda b}\end{aligned}}\right. \Longleftrightarrow \left\{{\begin{aligned}&{x=x_A+\lambda a}\\&{y=y_A+\lambda b}\end{aligned}}\right.$
Ce dernier système forme une représentation paramétrique de la droite D.
2. Représentation paramétrique d'une droite définie à l'aide d'une équation cartésienne
Considérons une droite D dont une équation cartésienne est : $ax+by+c=0$ où a, b et c sont des réels tels que $(a,b) \neq (0,0)$
Supposons $b \neq 0$
Alors $y=- \frac ab x- \frac cb $. Posons $x= \lambda$ alors $y=- \frac ab \lambda- \frac cb $ donc une représentation paramétrique de D est : $\left\{{\begin{aligned}&{x=\lambda}\\&{y=- \tfrac ab \lambda- \tfrac cb}\end{aligned}} \;\; \lambda \in \Bbb R \right.$
Supposons $b \neq 0$
Alors $y=- \frac ab x- \frac cb $. Posons $x= \lambda$ alors $y=- \frac ab \lambda- \frac cb $ donc une représentation paramétrique de D est : $\left\{{\begin{aligned}&{x=\lambda}\\&{y=- \tfrac ab \lambda- \tfrac cb}\end{aligned}} \;\; \lambda \in \Bbb R \right.$
Autres articles
Fonction logarithme népérien
Etude de fonctions
Cryptographie
Probabilité conditionnelle
Identité de Bezout
Divisibilité dans ℤ
Le triangle de Pascal
Les nombres de Mersenne
Théorie des situations
Evaluation du travail de l'élève
Les théories de l'apprentissage
Eléments de logique mathématiques
Fractales (Partie I) - Arbres fractales
Fractales (Partie II) - Plantes fractales
Fractales (Partie III) - Courbes et formes fractales
Fractales (Partie IV) - Ensemble de Mandelbrot
MathJax - Beautiful math in all browsers
Dénombrement
Droite dans le plan
Etude de fonctions
Cryptographie
Probabilité conditionnelle
Identité de Bezout
Divisibilité dans ℤ
Le triangle de Pascal
Les nombres de Mersenne
Théorie des situations
Evaluation du travail de l'élève
Les théories de l'apprentissage
Eléments de logique mathématiques
Fractales (Partie I) - Arbres fractales
Fractales (Partie II) - Plantes fractales
Fractales (Partie III) - Courbes et formes fractales
Fractales (Partie IV) - Ensemble de Mandelbrot
MathJax - Beautiful math in all browsers
Dénombrement
Droite dans le plan
Dhaouadi Nejib13-08-2019 22:18:18
Bonjour hijazi lalla rabia
Merci de prendre le temps de lire cet article que j'ai élaboré en faveur d'un élève qui trouve des difficultés en manipulant la droite dans le plan et ses équations.
Merci aussi pour vos remarques et vos questions qui me semblent sérieux et qui méritent des réponses.
1) J'ai signalé dans I. (Introduction) que dans la suite le repère est cartésien. Alors que dans III.5. j'ai signalé que le repère est orthonormé en effet le contenu proposé l'exige. Mais parfois, en faisant une figure, on utilise un logiciel où le repère est toujours orthogonal et personnellement je ne vois aucun problème.
2) Dans l'exercice 2, j'ai donné un schéma qui montre un trapèze donc je ne peut pas dire "ABCD un quadrilatère" alors que l'élève vois un trapèze (je sais qu'un trapèze est un quadrilatère). Bien sure l'objectif de l'exercice n'a aucun rapport avec la nature du quadrilatère, mais peut être je suis influencé par l'objectif implicite "intersection des diagonales". Finalement, je vois que vous avez raison, j'aurais du donné un quadrilatère qcq.
3) Pour la donnée d'une figure géométrique:
Parfois on peut donner une figure géométrique pour aider l'élève à assimiler les données de l'exercice ou encore pour aider l'élève à vérifier les résultats trouvés (c'est le cas de l'ex 1, il suffit de tracer les diagonales)
Finalement c'est le professeur qui décide en fonction de plusieurs facteurs.
Merci de prendre le temps de lire cet article que j'ai élaboré en faveur d'un élève qui trouve des difficultés en manipulant la droite dans le plan et ses équations.
Merci aussi pour vos remarques et vos questions qui me semblent sérieux et qui méritent des réponses.
1) J'ai signalé dans I. (Introduction) que dans la suite le repère est cartésien. Alors que dans III.5. j'ai signalé que le repère est orthonormé en effet le contenu proposé l'exige. Mais parfois, en faisant une figure, on utilise un logiciel où le repère est toujours orthogonal et personnellement je ne vois aucun problème.
2) Dans l'exercice 2, j'ai donné un schéma qui montre un trapèze donc je ne peut pas dire "ABCD un quadrilatère" alors que l'élève vois un trapèze (je sais qu'un trapèze est un quadrilatère). Bien sure l'objectif de l'exercice n'a aucun rapport avec la nature du quadrilatère, mais peut être je suis influencé par l'objectif implicite "intersection des diagonales". Finalement, je vois que vous avez raison, j'aurais du donné un quadrilatère qcq.
3) Pour la donnée d'une figure géométrique:
Parfois on peut donner une figure géométrique pour aider l'élève à assimiler les données de l'exercice ou encore pour aider l'élève à vérifier les résultats trouvés (c'est le cas de l'ex 1, il suffit de tracer les diagonales)
Finalement c'est le professeur qui décide en fonction de plusieurs facteurs.
hijazi lalla rabia13-08-2019 16:50:49
Bonjour,
je trouve que le travail est bien présenté et ses objectifs déclarés sont aussi précis et respectés. néanmoins j'ai quelques remarques:
un repère cartésien est il toujours orthogonal? orthonormé?
Pour l'exercice 1, quelle est l'utilité de mentionner le quadrilatère ABCD et sa nature pour répondre aux questions posées?
pour l'exercice 2, on ne voit pas le repère sur la figure géométrique.
La dernière remarque est une question: le fait de donner une figure géométrique dans un exercice, n'influence-t-il pas la réponse de l'élève ?
Merci pour votre compréhension
je trouve que le travail est bien présenté et ses objectifs déclarés sont aussi précis et respectés. néanmoins j'ai quelques remarques:
un repère cartésien est il toujours orthogonal? orthonormé?
Pour l'exercice 1, quelle est l'utilité de mentionner le quadrilatère ABCD et sa nature pour répondre aux questions posées?
pour l'exercice 2, on ne voit pas le repère sur la figure géométrique.
La dernière remarque est une question: le fait de donner une figure géométrique dans un exercice, n'influence-t-il pas la réponse de l'élève ?
Merci pour votre compréhension
Connectez vous pour ajouter des commentaires.
Commentaires