Cryptographie
Dhaouadi Nejib

I. Introduction
II. Cryptographie
III. Exemples de cryptographie symétrique
IV. Le RSA un exemple de cryptographie asymétrique
V. Fonction de Hachage
VI. Sécurité et attaques des systèmes actuels
VII. Les applications de la cryptographie
II. Cryptographie
III. Exemples de cryptographie symétrique
IV. Le RSA un exemple de cryptographie asymétrique
V. Fonction de Hachage
VI. Sécurité et attaques des systèmes actuels
VII. Les applications de la cryptographie
I. Introduction
D'après le Petit Robert de la langue française 2007,le cryptage est une Opération par laquelle un message est rendu inintelligible à quiconque ne possède pas la clé permettant de retrouver la forme initiale.D'après wikipedia, Le chiffrement ou cryptage est un procédé de cryptographie grâce auquel on souhaite rendre la compréhension d'un document impossible à toute personne qui n'a pas la clé de (dé)chiffrement. Ce principe est généralement lié au principe d'accès conditionnel.
Les opérations de chiffrement et de codage font partie de la théorie de l'information et de la théorie des codes. La différence essentielle réside dans la volonté de protéger les informations et d'empêcher des tierces personnes d'accéder aux données dans le cas du chiffrement.
Le codage consiste à transformer de l'information (des données) vers un ensemble de mots. Chacun de ces mots est constitué de symboles.
La compression est un codage : on transforme les données vers un ensemble de mots adéquats destinés à réduire la taille mais il n'y a pas de volonté de dissimuler (bien que cela se fasse implicitement en rendant plus difficile d'accès le contenu).
Le « code » dans le sens cryptographique du terme travaille au niveau de la sémantique (les mots ou les phrases). Par exemple, un code pourra remplacer le mot « avion » par un numéro. Le chiffrement travaille sur des composantes plus élémentaires du message, les lettres ou les bits, sans s'intéresser à la signification du contenu. Un code nécessite une table de conversion, aussi appelée « dictionnaire » (codebook en anglais). Ceci étant, « code » et « chiffrement » sont souvent employés de manière synonyme malgré cette différence.
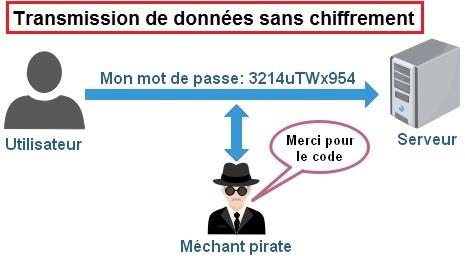
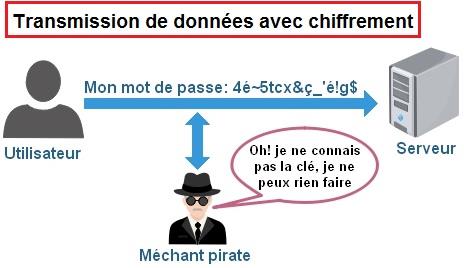
L'art de définir des codes est la cryptographie (un spécialiste de cryptographie est un cryptographe).
L'art de casser des chiffres est la cryptologie ou cryptanalyse (un spécialiste de cryptanalyse est un cryptanalyste, cryptologue ou casseur de codes)
Un cryptosystème est l'ensemble des deux méthodes de chiffrement et de déchiffrement utilisable en sécurité.
Au cours des siècles, de nombreux systèmes de chiffrage ont été inventés, tous de plus en plus perfectionnés, et il est vrai que l’informatique y a beaucoup contribué. Mais au commencement les algorithmes étaient loin d’être aussi complexes et astucieux qu’à notre époque. La majeure partie des méthodes de chiffrement reposait sur deux principes fondamentaux : la substitution (remplacer certaines lettres par d’autres) et la transposition (permuter des lettres du message afin de le brouiller).
II. Cryptographie
1. La cryptographie symétrique
On parle de cryptographie symétrique lorsqu'un texte, document, etc. est chiffré et déchiffré avec la même clé, la clé secrète. Ce procédé est à la fois simple et sûr.Principal inconvénient : étant donné que l'on n'a qu'une clé, si vous la donnez à X pour qu'il puisse vous envoyer des messages chiffrés avec celle-ci, il pourra aussi bien déchiffrer tous les documents que vous avez chiffrés avec cette dernière. La clé est donc connue uniquement par le destinataire et l'émetteur et il est plus sûr de faire une clé pour un échange entre X et Y, pour éviter qu'avec une clé on puisse tout déchiffrer.
2. La cryptographie asymétrique
Contrairement à la cryptographie symétrique, ici avec l'asymétrique, on a 2 clés.Tout d'abord nous avons la clé publique. Celle-ci, tout le monde peut la posséder, il n'y a aucun risque, vous pouvez la transmettre à n'importe qui. Elle sert à chiffrer le message. Puis il y a la clé privée que seul le récepteur possède, en l'occurrence vous. Elle servira à déchiffrer le message chiffré avec la clé publique.
3. Cryptographie à sens unique
Une fonction de hachage cryptographique est une fonction de hachage qui, à une donnée de taille arbitraire, associe une image de taille fixe, et dont une propriété essentielle est qu'elle est pratiquement impossible à inverser, c'est-à-dire que si l'image d'une donnée par la fonction se calcule très efficacement, le calcul inverse d'une donnée d'entrée ayant pour image une certaine valeur se révèle impossible sur le plan pratique. Pour cette raison, on dit d'une telle fonction qu'elle est à sens unique.La donnée d'entrée de ces fonctions est souvent appelée message ; la valeur de sortie est souvent appelée valeur de hachage, empreinte numérique, empreinte, ou encore haché (en anglais, message digest ou digest, hash).
III. Exemples de cryptographie symétrique
1. Chiffrement de César
Il a fallut attendre 200 avant JC pour voir naître le premier vrai système de cryptage. Il s’agit du code de César, ou chiffre de César, en référence à Jules César.Pour utiliser le code de César, il suffit d'aligner toutes les lettres de l'alphabet, et de remplacer chaque lettre du message clair par une autre lettre à une distance fixe notée n. Par exemple, avec n = 3, a devient d, b devient e, etc...
| A | B | C | D | E | F | G | H | I | ... |
| D | E | F | G | H | I | J | K | L | ... |
On peut étendre cette méthode de César aux 128 caractères ASCII ou les 256 caractères ASCII et extended ASCII ou plus encore tous les 4096 premiers caractères unicode représentant la plupart des caractères courants et latins, en particulier les caractères arabe (les 128 premiers caractères utilisent 1 byte et les autres 2 bytes)
Voici les deux fonctions de cryptage et décryptage suivant la méthode de César, en programmation vb.net
Function EncryptCesar(ByVal s As String, ByVal clef As Integer) As String
Dim retValue As String = ""
Dim c() As Char = s.ToCharArray()
For Each cc In c
retValue = retValue & ChrW((AscW(cc) + clef) Mod 4096)
Next
Return retValue
End Function
Function DecryptCesar(ByVal s As String, ByVal clef As Integer) As String
Dim retValue As String = ""
Dim c() As Char = s.ToCharArray()
For Each cc In c
retValue = retValue & ChrW((AscW(cc) - clef + 4096) Mod 4096)
Next
Return retValue
End Function
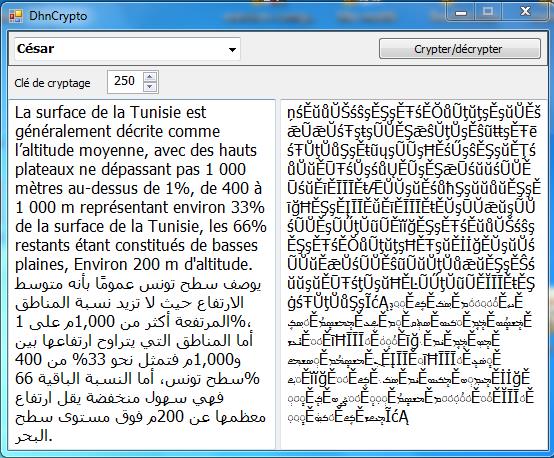
D'ailleurs, Le code de césar est toujours utilisé à l'heure actuelle, mais à changé de nom ! On l'appelle à présent ROT-13.
Le ROT-13 fonctionne exactement comme le chiffre de César, sauf que le décalage est toujours de 13. Ainsi, a devient n, b devient o, etc...
Le chiffrement de César est probablement le chiffrement de substitution le plus connu, mais ce n’est pas le seul. Tous les chiffrements de substitution fonctionnent de la même manière : en substituant chaque lettre dans le texte brut d’une lettre dans le texte chiffré, avec une relation un-à-un entre le texte brut et texte chiffré. Regardons quelques autres chiffrements de substitution.
2. Chiffrement Atbash
Les scribes hébreux ont utilisé le chiffrement de substitution Atbash. L’application du chiffrement Atbash est assez simple: il suffit d’inverser l’ordre des lettres du alphabet. C’est, selon les normes modernes, un chiffrement très primitif qui est facile à casser. Pour par exemple, en anglais, a devient z, b devient y, c devient x, et ainsi de suite. Bien sûr, les Hébreux utilisaient l’alphabet hébreu, aleph étant la première lettre et tav la dernière lettre.Exemple : Le message "BAC" devient "YZX"
| A | B | C | D | E | F | G | H | I | J | K | L | M |
| Z | Y | X | W | V | U | T | S | R | Q | P | O | N |
| N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| M | L | K | J | I | H | G | F | E | D | C | B | A |
3. Le Grand Chiffrement
Le Grand Chiffrement est un nomenclateur célèbre utilisé par le gouvernement Français jusqu’au début des années 1800. Ce chiffrement a été inventé par la famille Rossignol, une famille Français avec plusieurs générations de cryptographes, qui ont tous servi la cour Français. Le premier, un Mathématicien Rossignol de 26 ans, a servi sous Louis XIII, créant des codes sécurisés.
Le Grand Chiffrement utilisait 587 nombres différents qui représentaient des syllabes (notez qu’il y avait des variations sur ce thème, certaines avec un nombre de codes différent). Pour aider à prévenir l'analyse de fréquence, le texte chiffré inclurait des valeurs NULL, ou des nombres qui ne signifiaient rien. Il y avait aussi des pièges, ou des codes qui indiquaient que le destinataire devait ignorer le message précédent.
4. Chiffrement Polybien
Le chiffrement de Polybe (également connu sous le nom de carré de Polybe) a été inventé par les Grecs. l’historien Polybe (vers 200-118 av. J.C.-C.). De toute évidence, son travail utilisait l’alphabet grec, mais nous l’utiliserons avec l’anglais ici. Comme le montre la grille suivante, dans le chiffrement de Polybe, chaque lettre est représentée par deux chiffres. Ces deux nombres étant le x et le y coordonnées de cette lettre sur la grille. Par exemple, A est 11, T est 44, C est 13 et K est 25. Donc, pour chiffrer le mot "attaque", vous utiliseriez 114444111325.
Malgré l’utilisation de deux chiffres pour représenter une seule lettre, il s’agit d’un chiffrement de substitution et maintient toujours les fréquences de lettres et de mots trouvées dans la langue sous-jacente du texte brut.
Si vous avez utilisé le carré standard de Polybe, qui est un chiffre largement connu, il se fissurerait facilement, même sans aucune analyse de fréquence. L'utilisation d'un codage différent pour les lettres dans le carré nécessite le partage du carré particulier de Polybe à l’avance, afin qu’on puisse envoyer et lire des messages.
| 1 | 2 | 3 | 4 | 5 | |
| 1 | A | B | C | D | E |
| 2 | F | G | H | I/J | K |
| 3 | L | M | N | O | P |
| 4 | Q | R | S | T | U |
| 5 | V | W | X | Y | Z |
5. Chiffrement affine
C'est une méthode de chiffrement symétrique qui à chaque caractère ASCII ou ASCII extended (en particulier les lettres de l’alphabet), on associe son code qui est un nombre entier m compris entre 0 et 255.On choisit une expression affine de la forme ax+b modulo n où a et b des entiers et n un entier positif tel que $pgcd(a,n)=1$
Etude d'un exemple
Prenons dans cet exemple a=17, b=5 et n=4096
On définit le procédé de codage de la façon suivante:
- m étant le code (entier) d'un caractère donné dans la table des caractères unicode (dans cet exemple, on prend les 4096 premiers caractères y compris les caractères arabe de 1536 jusqu'à 1791)
- On calcule le reste p de la division Euclidienne de 17m+5 par 4096
- Au nombre p on associe le caractère correspondant dans la table des caractères unicode
Ainsi pour décoder, il suffit de correspondre au caractère de code p le caractère de code le reste de la division Euclidienne de 241p+2891 par 4096.
Voici, en language vb.net, le programme de chiffrement et de déchiffrement utilisant l'exemple ci dessus.
Function EncryptAffine(ByVal s As String) As String
Dim retValue As String = ""
Dim c() As Char = s.ToCharArray()
For Each cc In c
Dim mm As Integer = AscW(cc)
Dim p As Integer = (17 * mm + 5) Mod 4096
retValue = retValue & ChrW(p)
Next
Return retValue
End Function
Function DecryptAffine(ByVal s As String) As String
Dim retValue As String = ""
Dim c() As Char = s.ToCharArray()
For Each cc In c
Dim mm As Integer = AscW(cc)
Dim p As Integer = (241 * mm + 2891) Mod 4096
retValue = retValue & ChrW(p)
Next
Return retValue
End Function
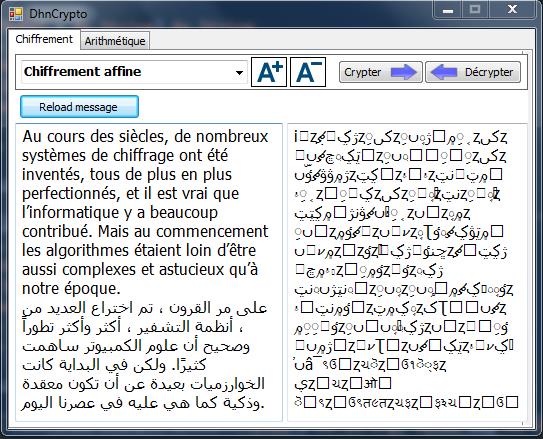
6. Chiffrement de vigenère
Le chiffre de Vigenère est un système de chiffrement poly alphabétique, c'est un chiffrement par substitution, mais une même lettre du message clair peut, suivant sa position dans celui-ci, être remplacée par des lettres différentes, contrairement à un système de chiffrement mono alphabétique comme le chiffre de César.Le chiffrement de Vigenère est un cryptosystème symétrique, ce qui signifie qu'il utilise la même clé pour le chiffrement et le déchiffrement. Il utilise une clé plus longue afin de pallier le principal problème du chiffrement de César: le fait qu'une lettre puisse être codée d'une seule façon.
Pour cela on utilise un mot clé au lieu d'un simple caractère.
On associe dans un premier temps à chaque lettre un code correspondant.
| A | B | C | D | E | F | G | H | I | J | K | L | M |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
Par exemple le texte "RENDEZVOUS" avec la clé "BONJOUR" sera codé de la manière suivante :
| Texte | R | E | N | D | E | Z | V | O | U | S |
| code P | 17 | 4 | 13 | 3 | 4 | 25 | 21 | 14 | 20 | 18 |
| clé | B | O | N | J | O | U | R | B | O | N |
| code K | 1 | 14 | 13 | 9 | 14 | 20 | 17 | 1 | 14 | 13 |
| Crypté | 18 | 18 | 0 | 12 | 18 | 19 | 12 | 15 | 8 | 5 |
| Code C | S | S | A | M | S | T | M | P | I | F |
R E N D E Z V O U S
Clé:
B O N J O U R
Texte crypté:
S S A M S T M P I F
La formule utilisée est : $C\equiv P+K$ (mod 26)
Pour déchiffrer ce message il suffit d'avoir la clé secrète et faire le déchiffrement inverse, à l'aide d'une soustraction $P\equiv C-K$ (mod 26).
Bien que ce chiffrement soit beaucoup plus sûr que le chiffrement de César, il peut encore être facilement cassé. En effet, lorsque les messages sont beaucoup plus longs que la clé, il est possible de repérer la longueur de la clé et d'utiliser pour chaque séquence de la longueur de la clé la méthode consistant à calculer la fréquence d'apparition des lettres, permettant de déterminer un à un les caractères de la clé...
Pour éviter ce problème, une solution consiste à utiliser une clef dont la taille est proche de celle du texte afin de rendre impossible une étude statistique du texte crypté. Ce type de système de chiffrement est appelé système à clé jetable. Le problème de ce type de méthode est la longueur de la clé de cryptage (plus le texte à crypter est long, plus la clé doit être volumineuse), qui empêche sa mémorisation et implique une probabilité d'erreur dans la clé beaucoup plus grande (une seule erreur rend le texte indéchiffrable...).
IV. Le RSA un exemple de cryptographie asymétrique
1. L’arithmétique pour RSA
☛ Théorème 1 (Petit théorème de Fermat)
Si p est un entier naturel premier et $a \in \Bbb Z$ alors $a^p \equiv a \;\; (mod\;p) $
☛ Corollaire 1
Si p ne divise pas a alors $a^{p-1} \equiv 1 \;\; (mod\;p) $
☛ Théorème 2
Démonstration
Soient a et b deux entiers non tous nuls
Si $d=pgcd(a,b)$ alors il existe deux entiers u et v tels que $d=au+bv$
Si $d=pgcd(a,b)$ alors il existe deux entiers u et v tels que $d=au+bv$
Notons S l'ensemble des entiers de la forme $au+bv$ où u et v deux entiers tels que au+bv>0
Supposons $a\neq 0$ et prenons $u=1 (si\;a>0)$ ou $u=-1 (si \;a<0 )$ et $v=0$
Alors $|a|=a\times u+b\times 0$ ⇒ $|a|\in S$⇒ $S\neq ∅$
Soit d le plus petit élément de S
$d\in S\Longrightarrow$ il existe deux entiers $u_0$ et $v_0$ tels que $d=au_0+bv_0$
Faisons la division euclidienne de a par d, alors il existe deux entiers q et r tels que $a=dq+r$ où $0\leqslant r< d$
Donc $r=a-qd=a-q(au_0+bv_0)$ $=a(1-qu_0)+b(-qv_0)>0$ $\Longrightarrow r\in S$ avec $0\leqslant r< d$
Or d étant le plus petit élément de S donc $r=0$ et par suite $a=qd$
On montre aussi de la meme façons que $b=q'd$
Alors d est un diviseur commun de a et b (*)
Soit c un entier naturel non nul, diviseur commun de a et b donc c divise $au_0+bv_0=d$ c-à-d c divise d (**)
(*) et (**) $\Longrightarrow d=pgcd(a,b)$
☛ Corollaire 2 (Identité de Bezout)
Démonstration
Soient a et b deux entiers non nuls
$pgcd(a,b)=1$ si et seulement si il existe deux entiers u et v tels que $au+bv=1$
$pgcd(a,b)=1$ si et seulement si il existe deux entiers u et v tels que $au+bv=1$
$pgcd(a,b)=1$ donc d'après théorème 3, il existe deux entiers u et v tels que $au+bv=1$
Réciproquement
Supposons quad'il existe deux entiers u et v tels que $au+bv=1$ et soit $d=pgcd(a,b)$
d divise a et b donc d divise $au+bv$ alors d divise 1 d'où $d=1$
☛ Corollaire 3
Démonstration
Soient a, b et n des entiers
$pgcd(a,n)=1$ et $pgcd(b,n)=1$ $\Longleftrightarrow pgcd(ab,n)=1$
$pgcd(a,n)=1$ et $pgcd(b,n)=1$ $\Longleftrightarrow pgcd(ab,n)=1$
$pgcd(a,n)=1\Longrightarrow$ il existe deux entiers $u_1$ et $v_1$ tels que $au_1+nv_1=1$
$pgcd(b,n)=1\Longrightarrow$ il existe deux entiers $u_2$ et $v_2$ tels que $bu_2+nv_2=1$
Alors $1=(au_1+nv_1)(bu_2+nv_2)$ $=ab(u_1u_2)$ $+n(au_1v_2+bu_2v_1+nv_1v_2)$
Donc d'après l'identité de Bezout $pgcd(ab,n)=1$
Réciproquement
On peut utiliser facilement l'identité de Bezout
$pgcd(ab,n)=1$ $\Longrightarrow abu+vn=1$ ce qu'on peut l'écrire $as+vn=1$ ou $bt+vn=1$ donc $pgcd(a,n)=1$ et $pgcd(b,n)=1$
☛ Corollaire 4
Démonstration
Soient $a_1$ $a_2$ ... $a_p$ et n des entiers
Si on a $\forall i\in\left\{{1,2,...,p}\right\}$ $pgcd(a_i,n)=1$
Alors $pgcd\left(\,\prod\limits_{i=1}^{p}{a_i}\,,\,n \right)=1$
Si on a $\forall i\in\left\{{1,2,...,p}\right\}$ $pgcd(a_i,n)=1$
Alors $pgcd\left(\,\prod\limits_{i=1}^{p}{a_i}\,,\,n \right)=1$
Il suffit de raisonner par récurrence en utilisant le théorème 3
L’algorithme d’Euclide étendu
Nous savons déjà l’algorithme d’Euclide qui repose sur le principe que pgcd(a, b) = pgcd(b, a (mod b)).Nous pouvons alors « remonter » l’algorithme d’Euclide à la main pour obtenir les coefficients de Bézout s, t tels que as + bt = pgcd(a, b). Cependant il nous faut une méthode plus automatique pour obtenir ces coefficients, c’est l’algorithme d’Euclide étendu.
On définit deux suites ($s_i$), ($t_i$) qui vont aboutir aux coefficients de Bézout.
L’initialisation est : $s_0=1$ $s_1=0$ $t_0=0$ $t_1=1$
et la formule de récurrence pour $i \geqslant 1$ : $s_{i+1} = s_{i−1} − q_i s_i$ et $t_{i+1} = t_{i−1} − q_i t_i$ où $q_i$ est le quotient de a par b dans l'iteration de l'algorithme d'Euclide.
Algorithme
$a_0\;\longleftarrow a$$b_0\;\longleftarrow b$
$t_0\;\longleftarrow 0$
$t\;\longleftarrow 1$
$s_0\;\longleftarrow 1$
$s\;\longleftarrow 0$
$q\;\longleftarrow \left[{\frac{a_0}{b_0}}\right]$
$r\;\longleftarrow a_0-qb_0$
While r>0
Do $ \left\{ \begin{array}{l} temp \;\longleftarrow \;t_0-qt\\ t_0 \;\longleftarrow \;t\\ t \;\longleftarrow \;temp \\ temp \;\longleftarrow \; s_0-qs \\ s_0 \;\longleftarrow \; s \\ s \;\longleftarrow \; temp \\ a_0 \;\longleftarrow \; b_0 \\ b_0 \;\longleftarrow \; r \\ q \;\longleftarrow \; \left[{\frac{a_0}{b_0}}\right] \\ r \;\longleftarrow \; a_0-b_0q \\ \end{array} \right. $
$ r \;\longleftarrow \; b_0 \\ Return (r,s,t) $ Application de cet algorithme avec le language vb.net
Programme en vb.net
Function euclide_etendu(ByVal a As BigInteger, ByVal b As BigInteger) As BigInteger()
Dim a0 As BigInteger = a
Dim b0 As BigInteger = b
Dim t0 As BigInteger = BigInteger.Zero
Dim t As BigInteger = BigInteger.One
Dim s0 As BigInteger = BigInteger.One
Dim s As BigInteger = BigInteger.Zero
Dim q As BigInteger = BigInteger.Divide(a0, b0)
Dim r As BigInteger = a0 - q * b0
While r > BigInteger.Zero
Dim tmp As BigInteger = t0 - q * t
t0 = t
t = tmp
tmp = s0 - q * s
s0 = s
s = tmp
a0 = b0
b0 = r
q = BigInteger.Divide(a0, b0)
r = a0 - q * b0
End While
r = b0
Dim retval(2) As BigInteger
retval(0) = r : retval(1) = s : retval(2) = t
Return retval
End Function
Inverse modulo n
Soit $a \in \Bbb Z$, on dit que $x \in \Bbb Z$ est un inverse de a modulo n si $ax\equiv 1 \;\; (mod n)$
☛ Théorème 3
Démonstration
Un entier $a$ admet un inverse modulo $n$ ($n\geqslant 2$) si et seulement si $pgcd(a,n)=1$.
pgcd(a,n)=1 $⟺$ ∃u, v ∈ ℤ tq au+nv=1 (Th. Bézout)
⟺ ∃u ∈ ℤ tq au ≡ 1 (mod n)
Function InverseModn(ByVal a As BigInteger, ByVal n As BigInteger) As BigInteger
Dim auv() As BigInteger = euclide_etendu(a, n)
If auv(0) <> BigInteger.One Then
Return BigInteger.Zero
Else
Dim r As BigInteger = auv(1) Mod n
If r < BigInteger.Zero Then r = r + n
Return r
End If
End Function
☛ Définition
On appelle $\Phi-fonction$ d'Euler la fonction qui à tout entier naturel n non nul associe le nombre des entiers j tels que $1\leqslant j \leqslant n$ et $pgcd(j,n)=1$
Exemples
➤$\Phi(3)=2 (j=1 et j=2)$➤$\Phi(4)=2 (j=1 et j=3)$
➤$\Phi(5)=4 $ $(j=1, j=2, j=3 et j=4)$
➤$\Phi(10)=4 $ $(j=1, j=3, j=7 et j=9)$
➤$\Phi(11)=10 $
➤$\Phi(12)=4 $
➤$\Phi(13)=12 $
Remarque
Si n est premier alors $\Phi(n)=n-1$
☛ Théorème 4(Théorème d'Euler)
Soient a et n deux entiers naturels non nuls
$pgcd(a,n)=1$ $\Longrightarrow a^{\Phi(n)}\equiv 1$ (mod n)
$pgcd(a,n)=1$ $\Longrightarrow a^{\Phi(n)}\equiv 1$ (mod n)
☛ Lemme
Soient n et b deux entiers naturels non nuls tels que $pgcd(b,n)=1$
On note T l'ensemble des entiers j tels que $1\leqslant j \leqslant n$ et $pgcd(j,n)=1$ et bT l'ensemble des nombres bt modulo n avec $t\in T$ alors tout élément de T est congru exactement à un seul élément de bT modulo n
On note T l'ensemble des entiers j tels que $1\leqslant j \leqslant n$ et $pgcd(j,n)=1$ et bT l'ensemble des nombres bt modulo n avec $t\in T$ alors tout élément de T est congru exactement à un seul élément de bT modulo n
Exemple
n=10 et b=7$T=\left\{{1,3,7,9}\right\}$ et $bT=\left\{{7,21,49,63}\right\}$ $\equiv \left\{{7,1,9,3}\right\}$ modulo 10
Soit $t\in T$ alors $pgcd(t,n)=1$ et $pgcd(b,n)=1$ donc d'après le corollaire 3 $pgcd(bt,n)=1$ alors il existe deux entiers u et v tels que $ubt+vn=1$
Soit c le reste modulo n de bt donc $bt\equiv c $ (mod n) alors $bt=c+kn$ où k est un entier et $1\leqslant c \leqslant n-1$ (car n ne divise pas bt)
$ubt+vn=1$ $\Longrightarrow u(c+kn)+vn=1$ $\Longrightarrow uc+(uk+v)n=1$ donc $pgcd(c,n)=1$ $\Longrightarrow c\in T$
Montrons que T et bT ont le même nombre d'éléments
Soient $t_1$ et $t_2$ deux éléments de T tels que $bt_1\equiv bt_2$ (mod n) alors $b(t_1-t_2) \equiv 0$ (mod n) avec $pgcd(b,n)=1$ donc $t_1-t_2 \equiv 0$ (mod n) ou encore $t_1\equiv t_2$ (mod n) ce qui prouve que T et bT ont le même nombre d'éléments
Démonstration du théorème d'Euler
Posons $T=\left\{{a_1,a_2,...,a_{\Phi(n)}}\right\}$ où $1\leqslant a_i \leqslant n$ et $pgcd(a_i,n)=1$D'après le lemme précédent chaque nombre $aa_i$ où $a_i\in T$ est congru exactement à un seul élément de T modulo n
Alors $(aa_1)(aa_2)...(aa_{\Phi(n)})$ $\equiv a_1a_2...a_{\Phi(n)}$ (mod n)
$\Longrightarrow a^{\Phi(n)}\prod\limits_{a_i\in T}{a_i}$ $\equiv \prod\limits_{a_i\in T}{a_i}$ (mod n) $\Longrightarrow (a^{\Phi(n)}-1)\prod\limits_{a_i\in T}{a_i}\equiv 0$ (mod n)
$\forall i \in \{1,2,...,\Phi(n)\}$ $\;\; pgcd(a_i,n)=1$ donc d'après corollaire 4, $pgcd(\prod\limits_{a_i\in T}{a_i},n)=1$ et finalement $a^{\Phi(n)}-1\equiv 0$ (mod n) ou encore $a^{\Phi(n)}\equiv 1$ (mod n) cqfd
Remarque
Notez que le théorème d’Euler généralise le théorème de Fermat puisque $\Phi(p) = p − 1$ et si a n’est pas un multiple de p, alors $pgcd(a, p) = 1$.
☛ Théorème 5
Démonstration
Soient p et q deux nombres premiers distincts et n=pq
Si e et d sont deux entiers naturels tels que $ed \equiv 1\; (mod\,\Phi(n))$ avec $\Phi(n)=(p-1)(q-1)$ alors :
Pour tout entier m, $m^{ed}\equiv m\; (mod\,n)$
Si e et d sont deux entiers naturels tels que $ed \equiv 1\; (mod\,\Phi(n))$ avec $\Phi(n)=(p-1)(q-1)$ alors :
Pour tout entier m, $m^{ed}\equiv m\; (mod\,n)$
$ed \equiv 1\; (mod\,\Phi(n))$ $\Longrightarrow ed=1+k\Phi(n)$ où k est un entier
➤ 1er Cas: p divise m
p divise m donc $m^{ed} \equiv m \equiv 0$ (mod p)
➤ 2ème Cas: p ne divise pas m
si p ne divise pas m alors d'après le théorème de Fermat $m^{p-1}\equiv 1$ (mod p)
$m^{ed}=m^{1+k\Phi(n)}$ $=m^{1+k(p-1)(q-1)}$ $=m\times (m^{p-1})^{k(q-1)}$ $\equiv m\times 1^{k(q-1)}\equiv m$ (mod p)
De la meme façon on montre que $m^{ed}\equiv m$ (mod q)
$m^{ed}\equiv m$ (mod p) et $m^{ed}\equiv m$ (mod q) ou encore $m^{ed}-m\equiv 0$ (mod p) et $m^{ed}-m\equiv 0$ (mod q) et puisque p et q sont deux nombres premiers distincts alors $pgcd(p,q)=1$ et par suite $m^{ed}-m\equiv 0$ (mod pq) c-à-d $m^{ed}\equiv m$ (mod n) cqfd
2. Le chiffrement RSA
RSA est un sigle provenant des noms de ses inventeurs, qui sont respectivement Ron Rivest, Adi Shamir et Léonard Adleman.Supposons que Mr X a décidé d'envoyer un message chiffré par la méthode RSA à Mr Y.
Préalablement, Mr X a dèja choisi une clé publique pour le chiffrement et une clé privée pour le déchiffrement qui doit la passer à Mr Y. Donc Mr X, qui veut envoyer le message chiffré, possède la clé publique (que tout le monde peut l'avoir sans aucun problème) et Mr Y, qui veut déchiffrer le message reçu, possède la clé privée (c'est un code secret pour lui seul).
Regardons de plus près le travail de Mr X.
- Mr X crée deux nombres premiers p et q.
- Calcule l'entier $n=pq$
- Calcule $\varphi \left({n}\right)=\left({p-1}\right)\left({q-1}\right)$
- L'entier e tq: $ 0 < e < \varphi \left({n}\right)\; et \; pgcd(\varphi (n),e)=1 $
- L'entier d tq: $ 0 < d < \varphi (n) \; et \; ed\equiv 1 \left[{\varphi (n)}\right] $
3. Exemples de chiffrements RSA
Exemple 1:-
Mr X choisit les deux nombres premiers
p=101 et q=103 - $n=p \times q \Rightarrow$ n=10403
- $\varphi (n)=(p-1)(q-1) \Rightarrow$$\varphi$(n)=10200
- On cherche un entier e vérifiant :
$ 0 < e < \varphi \left({n}\right)\; et \; pgcd(\varphi (n),e)=1 $
On peut choisir, par exemple, e=107 - A l'aide de l'algorithme d'Euclide etendu, on peut trouver l'entier d inverse de e modulo $\varphi$(n)
d=5243 - Dans cet exemple:
La clé publique est:n=10403 et e=107
La clé privée est d=5243
-
Mr X choisit les deux nombres premiers
p=3598279 et q=7815629 - $n=p \times q \Rightarrow$ n=28122813702491
- $\varphi (n)=(p-1)(q-1) \Rightarrow$$\varphi$(n)=28122802288584
- On cherche un entier e vérifiant :
$ 0 < e < \varphi \left({n}\right)\; et \; pgcd(\varphi (n),e)=1 $
On peut choisir, par exemple, e=233 - A l'aide de l'algorithme d'Euclide etendu, on peut trouver l'entier d inverse de e modulo $\varphi$(n)
d=27519308677241 - Dans cet exemple:
La clé publique est:n=28122813702491 et e=233
La clé privée est d=27519308677241
-
Mr X choisit les deux nombres premiers
p=1234567877771 et q=1234567877759 - $n=p \times q \Rightarrow$ n=1524157844809175981395189
- $\varphi (n)=(p-1)(q-1) \Rightarrow$$\varphi$(n)=1524157844806706845639660
- On cherche un entier e vérifiant :
$ 0 < e < \varphi \left({n}\right)\; et \; pgcd(\varphi (n),e)=1 $
On peut choisir, par exemple, e=99991 - A l'aide de l'algorithme d'Euclide etendu, on peut trouver l'entier d inverse de e modulo $\varphi$(n)
d=1169362933307462828287011 - Dans cet exemple:
La clé publique est:n=1524157844809175981395189 et e=99991
La clé privée est d=1169362933307462828287011
On suppose que le message est écrit en anglais (pas de lettres accentuées)
Chaque lettre est représentée à l'aide d'un nombre de deux chiffres
A ----> 01, B ----> 02 ... Z ----> 26
Chiffrement à l'aide de l'exemple 2:
Notre message : "BAC"
Alors m=020103=20103 (B--->02, A--->01, C--->03)
$c\equiv m^e\equiv 20103^{233}$ $\equiv 19242634890428$ $\;(mod\,28122813702491)$
Donc c est le message chiffré appelé ciphertext, c'est le message que doit recevoir Mr Y
Déchiffrement du message:
Mr Y qui possède la clé privée d=27519308677241 peut déchiffrer le message de la manière suivante:
$m\equiv c^d \equiv 19242634890428^{27519308677241}$ $\equiv 20103 \;(mod \, 28122813702491)$.
Il reste à traduire ce nombre en texte à l'aide des numéros des lettres cités en haut.
Chiffrement à l'aide de l'exemple 3:
Notre message : "MATH" Alors m=13012008 (M--->13, A--->01, T--->20, H--->08)
n=1524157844809175981395189 ; d=1169362933307462828287011 et e=99991
$c\equiv m^e\equiv 13012008^e$ $\equiv 646459942194413367430228 \;(mod\,n)$
Donc c est le ciphertext, c'est le message que doit recevoir Mr Y
Déchiffrement du message:
Mr Y qui possède la clé privée d peut déchiffrer le message de la manière suivante:
$m\equiv c^d \equiv 646459942194413367430228^d$ $ \equiv 13012008 \;(mod \, n)$.
Il reste à traduire ce nombre en texte à l'aide des numéros des lettres cités en haut.
Remarques
Si le message de Mr X est plus grand que n, alors il doit être divisé en morceaux (ou blocs), chaque morceau étant plus petit que n.C'est pour cette raison que j'ai chiffré et déchiffré les messages "BAC" et "MATH" à l'aide des exemples 2 et 3 alors que l'exemple 1 est incappable de le faire car n=10403 est inferieur à m dans les deux cas.
4. Factorization
Le problème de factorisation des entiers est le problème de décomposer un entier positif n en facteurs non négligeables (de préférence premiers). La multiplication des entiers est instantanément exécutée sur n'importe quel ordinateur. Mais l'opération inverse, c'est-à-dire factorisation, est difficile sur le plan du calcul. Ce problème de factorisation des entiers joue un rôle très important dans le domaine de cryptologie. En général, les temps de fonctionnement des algorithmes d'affacturage sont des fonctions de la taille de n seulement. Dans certains cas particuliers, ces temps peuvent également dépendre de certaines propriétés spécifiques de n, par exemple, sur la taille des facteurs principaux de n. Il est conseillé d'essayer les algorithmes pour trouver les petits facteurs premiers d'abord. Le cas le plus difficile est quand n est le produit de deux nombres premiers de la même taille à peu près. En 1991, un concours mondial a été lancé, le RSA Factoring Challenge12 organisé par RSA Security afin de stimuler la communauté scientifique à étudier des algorithmes efficaces pour l'affacturage des grands entiers. Une liste de nombres a été publiée, qui étaient connus pour être les produits de deux nombres premiers. Ces numéros sont appelés numéros RSA. Un prix en espèces a été offert pour la factorisation de certains d'entre eux. Le premier, un numéro RSA-100 à 100 chiffres a été éliminé en quelques jours, mais la plupart d'entre eux restent intacts. Le concours a duré seize ans et a été officiellement clôturé en mai 2007. Certains des plus petits prix avaient été décernés à l'époque. Les prix restants ont été rétractés. De nombreux nombres ont été pris en compte pendant le défi. Aujourd'hui encore, ces résultats déterminent encore les limites d'une factorisation réalisable. Voici quelques détails du défi. En août 1999, la communauté cryptologique a été électrifiée pour apprendre qu'un nombre de 512 bits (155 chiffres décimaux) a été transformé en facteurs premiers.
10941738641570527421809707322040357612003732945449205990913842131476349984288934784717997257891267332497625752899781833797076537244027146743531593354333897.
'Il s'est avéré être le produit des deux nombres premiers à 78 chiffres décimaux suivants:
102639592829741105772054196573991675900716567808038066803341933521790711307779
×
106603488380168454820927220360012878679207958575989291522270608237193062808643En mars 2002, nCipher Inc. a annoncé qu’elle avait développé un logiciel qui abaissé pour briser la clé RSA 512 bits dans les six semaines, en utilisant des dizaines d'ordinateurs.
Un peu plus tard, le temps de calcul a été réduit à un jour. Ce sont évidemment de très bons résultats, mais il faut le noter et le souligner que l'augmentation du nombre de bits double l'espace de recherche. En décembre 2003, la factorisation du prochain numéro RSA Challenge a été annoncé. Cette fois, c'était RSA-576, un entier de 576 bits (174 chiffres décimaux). Cet entier est:
188198812920607963838697239461650439807163563379417382700763356422988859715234665485319060606504743045317388011303396716199692321205734031879550656996221305168759307650257059.
'C'est le produit de ces deux nombres premiers de 87 chiffres décimaux:
398075086424064937397125500550386491199064362342526708406385189575946388957261768583317
×
472772146107435302536223071973048224632914695302097116459852171130520711256363590397527.
1230186684530117755130494958384962720772853569595334792197322452151726400507263657518745202199786469389956474942774063845925192557326303453731548268507917026122142913461670429214311602221240479274737794080665351419597459856902143413
=
33478071698956898786044169848212690817704794983713768568912431388982883793878002287614711652531743087737814467999489
×
36746043666799590428244633799627952632279158164343087642676032283815739666511279233373417143396810270092798736308917Plus de numéros RSA attendent dans la file d'attente. Pour une personne qui parvient à décomposer le RSA-704, un prix de 30000\$ a été offert, et pour le numéro le plus long présenté, le RSA-2048, un US 200000\$.
Le numéro le plus long présenté au concours était le RSA-2048 (un nombre de 635 chiffres):
25195908475657893494027183240048398571429282126204032027777137836043662020707595556264018525880784406918290641249515082189298559149176184502808489120072844992687392807287776735971418347270261896375014971824691165077613379859095700097330459748808428401797429100642458691817195118746121515172654632282216869987549182422433637259085141865462043576798423387184774447920739934236584823824281198163815010674810451660377306056201619676256133844143603833904414952634432190114657544454178424020924616515723350778707749817125772467962926386356373289912154831438167899885040445364023527381951378636564391212010397122822120720357.
Les meilleurs algorithmes actuellement utilisés pour la factorisation des entiers de k bits ont la complexité temporelle. Le travail sur ces derniers et sur de nouveaux algorithmes ne donne pas beaucoup d'espoir pour une factorisation facile et rapide de grands nombres.
V. Fonction de Hachage
1. C'est quoi le hachage cryptographique?
Une fonction de hachage cryptographique est un algorithme qui prend une quantité arbitraire d’entrée de données et produit une sortie de taille fixe de texte chiffré appelée valeur de hachage, ou simplement « hachage ».
Un algorithme de hachage possède les propriétés suivantes:Non-réversibilité
Un bon hachage devrait rendre très difficile la reconstruction des données initiales (Input) à partir de la sortie ou du hachage (Output).
Diffusion
Un changement dans un seul bit des données initiales devrait entraîner un changement de la moitié des bits de son hachage. En d’autres termes, lorsque les données initiales sont légèrement modifiées, la sortie du texte chiffré devrait changer de manière significative.
Déterminisme
La donnée d'origine doit toujours générer la même valeur de hachage ou le même texte chiffré.
Résistance aux collisions
Il devrait être difficile de trouver deux données différentes qui hachent le même texte chiffré.
$h(d_1)=h(d_2)$ $\Longrightarrow d_1=d_2$
Imprévisible
La valeur de hachage ne doit pas être prévisible à partir des données initiales.
2. Exemples d'applications des hachages?
les hachages cryptographiques sont utilisés dans plusieurs domaines. Citons quelques exemples:❖ Intégrité des messages
Une utilisation courante des algorithmes de hachage consiste à garantir l’intégrité des messages. Évidemment les messages peuvent être modifiés pendant le transport, intentionnellement ou accidentellement. Vous pouvez utiliser le hachage pour détecter toute altération qui s’est produite.
Considérons, par exemple, un e-mail Message. Si vous placez le corps du message dans un algorithme de hachage (par exemple, SHA-1), la sortie est un hachage de 160 bits. Ce hachage peut être ajouté à la fin du message.
Les algorithmes de hachage MD5, SHA-1 ou SHA-2 sont parfois publiés sur des sites Web ou des forums pour permettre la vérification de l’intégrité des fichiers téléchargés, y compris les fichiers récupérés à l’aide du partage de fichiers tel que la mise en miroir.
Cette pratique établit une chaîne de confiance tant que les hachages sont publiés sur un site de confiance – généralement le site d’origine – authentifié par HTTPS. L’utilisation d’un hachage cryptographique et d’une chaîne de confiance détecte les modifications malveillantes apportées au fichier.
❖ Stockage de mots de passe
Les hachages cryptographiques offrent également un niveau de sécurité contre les menaces internes. Considérez le possibilité, par exemple, qu’une personne ayant accès à un système, tel qu’un réseau administrateur, a des intentions malveillantes. Cette personne peut simplement lire le mot de passe d’un utilisateur à partir de la base de données, puis utilisez les informations d’identification de connexion de cet utilisateur pour effectuer une attaque sur le système. Ensuite, si l’attaque est connue, c’est l’utilisateur final qui sera un suspect, et non l’administrateur qui est à l'origine de la violation. Une façon d’éviter cela consiste à stocker les mots de passe dans un hachage cryptographique. Lorsque l’utilisateur se connecte au système, quel que soit le mot de passe saisi, il est haché (produisant quelque chose comme ceci: 1DC190AB20139E1109E20977AFB1009A2379AGC9), puis comparé au hachage de la base de données, s'ils correspondent exactement, l’utilisateur est connecté au système.
Étant donné que la base de données stocke uniquement un hachage du mot de passe et que les hachages ne sont pas réversible, même un administrateur réseau ou un administrateur de base de données ne peut pas récupérer le mot de passe de la base de données. Si quelqu’un tente de taper le hachage comme mot de passe, le système hachera toute entrée placée dans le champ du mot de passe, produisant ainsi un hachage différent de celui stocké dans la base de données. Le stockage des mots de passe sous forme de hachage est largement répandu utilisé et fortement recommandé.
3. Les algorithmes des hachages populaires
➤ Message Digest (MD)MD5 était la fonction de hachage la plus populaire et la plus largement utilisée pendant plusieurs années. La famille MD comprend les fonctions de hachage MD2, MD4, MD5 et MD6. Il a été adopté en tant que norme Internet RFC 1321.
Il s’agit d’une fonction de hachage de 128 bits. Les résumés MD5 ont été largement utilisés dans le monde du logiciel pour fournir une assurance sur l’intégrité des fichiers transférés. Par exemple, les serveurs de fichiers fournissent souvent une somme de contrôle MD5 précalculée pour les fichiers, afin qu’un utilisateur puisse comparer la somme de contrôle du fichier téléchargé à celui-ci.
En 2004, des collisions ont été trouvées dans le MD5. Une attaque analytique n’a été détectée qu’en une heure à l’aide d’un cluster d’ordinateurs. Cette collision a entraîné une compromission du MD5 et, par conséquent, son utilisation n’est plus recommandée.
➤ Secure Hash Function (SHA)
La famille SHA comprend quatre algorithmes SHA; SHA-0, SHA-1, SHA-2 et SHA-3.
La version originale est SHA-0, une fonction de hachage de 160 bits, a été publiée par le National Institute of Standards and Technology (NIST) en 1993. Il avait peu de faiblesses et n’est pas devenu très populaire. Plus tard en 1995, SHA-1 a été conçu pour corriger les faiblesses présumées de SHA-0.
SHA-1 est la plus largement utilisée des fonctions de hachage SHA existantes. Il est utilisé dans plusieurs applications et protocoles largement utilisés, y compris la sécurité SSL (Secure Socket Layer).
En 2005, une méthode a été trouvée pour découvrir les collisions pour SHA-1 dans les délais pratiques, ce qui rend douteuse l’employabilité à long terme de SHA-1.
La famille SHA-2 a quatre autres variantes SHA, SHA-224, SHA-256, SHA-384 et SHA-512 en fonction du nombre de bits dans leur valeur de hachage. Aucune attaque réussie n’a encore été signalée sur la fonction de hachage SHA-2.
Bien que SHA-2 soit une fonction de hachage forte. Bien que significativement différent, sa conception de base suit toujours la conception de SHA-1. Par conséquent, le NIST (National Institute of Standards and Technology USA) a appelé à de nouvelles conceptions de fonctions de hachage compétitives.
En octobre 2012, le NIST a choisi l’algorithme Keccak comme nouvelle norme SHA-3. Keccak offre de nombreux avantages, tels que des performances efficaces et une bonne résistance aux attaques.
➤RIPEMD
RIPEMD est un acronyme pour RACE Integrity Primitives Evaluation Message Digest.
Cet ensemble de fonctions de hachage a été conçu par une communauté de recherche ouverte et généralement connu comme une famille de fonctions de hachage européennes. L’ensemble comprend RIPEMD, RIPEMD-128 et RIPEMD-160.
Il existe également des versions 256 et 320 bits de cet algorithme. RIPEMD d’origine (128 bits) est basé sur les principes de conception utilisés dans MD4 et s’avère fournir une sécurité douteuse.
La version 128 bits de RIPEMD est venue en remplacement rapide pour surmonter les vulnérabilités sur le RIPEMD d’origine. RIPEMD-160 est une version améliorée et la version la plus utilisée de la famille.
Les versions 256 et 320 bits réduisent le risque de collision accidentelle, mais n’ont pas de niveaux de sécurité plus élevés par rapport à RIPEMD-128 et RIPEMD-160 respectivement.
➤Whirlpool
Il s’agit d’une fonction de hachage 512 bits.
Il est dérivé de la version modifiée de Advanced Encryption Standard (AES). L’un des designers était Vincent Rijmen, co-créateur de l’AES.
Trois versions de Whirlpool ont été publiées; à savoir WHIRLPOOL-0, WHIRLPOOL-T et WHIRLPOOL.
VI. Sécurité et attaques des systèmes actuels
Les types d’attaques employés le plus couramment sont nombreux et diffèrents selon le type
du système (symétrique, asymétrique, fonction de hachage, etc…).Nous vous présentons ici une liste des types d’attaques sur les algorithmes :
• L'attaque en force (ou Brute force attack, Exhaustive key search attack)
Le cryptographe essaie toutes les combinaisons de clefs possibles jusqu'à l'obtention du texte clair. Avec des ordinateurs de plus en plus performants et des méthodes de calculs distribuées, l'attaque en force restera toujours un moyen de casser des systèmes de chiffrement.
• L'attaque à l'aide de l'analyse statistique (ou Statistical analysis attack)
Le cryptographe possède des informations sur les statistiques du message clair (fréquences des lettres ou des séquences de lettres). Les systèmes tels que ceux par substitution ne résistent pas à une telle attaque.
• L'attaque à l'aide de textes chiffrés seulement (ou Ciphertext-only attack)
Le cryptographe dispose de messages chiffrés par l'algorithme et fait des hypothèses sur le texte clair (présence d’expressions, de mots, le sens du message, format ASCII etc.). Il peut grâce à cela soit retrouvé les textes en clair, soit retrouver la clef.
• L'attaque à l'aide de textes clairs (ou Known-plaintext attack)
Le cryptographe dispose des messages ou parties des messages clairs et de leurs versions chiffrées. Le but du cryptographe est alors de retrouver la clef. Ce type d’attaque est très répandu.
• L'attaque à l'aide de textes clairs choisis (ou Chosen-plaintext attack)
Le cryptographe dispose des messages clairs et de leurs versions chiffrées. Il a aussi la possibilité de tester des messages et d'obtenir le résultat chiffré. Les chiffrements asymétriques sont notamment vulnérables à cette attaque.
• L'attaque d'une tierce personne (ou Man-in-the-middle attack)
Cette attaque plus communément appelée l’attaque de «l’homme du milieu» intervient dans une transaction entre deux personnes(groupes…). Une troisième personne s'interpose de manière transparente entre les deux et termine la transaction normalement en captant les messages et en transmettant d'autres messages. Il peut donc ainsi intercepter et même modifier les messages envoyés sans que les deux entités s'en aperçoivent. Cette attaque peut être évitée avec les signatures digitales.
• L'attaque à l'aide du temps d'opération (ou Timing Attack)
Cette méthode est basée sur la mesure du temps nécessaire pour effectuer des chiffrements ou des déchiffrements. Ainsi cette étude permet de mieux cibler la longueur de la clef utilisée et a donc pour but de limiter grandement le domaine des clefs à explorer pour une cryptanalyse classique.
VII. Les applications de la cryptographie
Cryptographie sur Internet L'une des utilisations les plus en vue de la cryptographie, du moins pour les utilisateurs d'Internet, est peut-être le protocole SSL (Secure Sockets Layer).
SSL est l'un des trois protocoles cryptographiques les plus importants pour établir un canal réseau sécurisé.
Internet est souvent modélisé comme une suite de protocoles Internet à quatre couches. Bien que SSL fonctionne au niveau de la couche de transport de la suite de protocoles Internet, des canaux sécurisés peuvent également être établis au niveau de la couche d'application supérieure à l'aide du protocole Secure Shell (SSH) et au niveau de la couche Internet inférieure à l'aide de "Internet Protocol Security" (IPS).
SSL est un protocole général de sécurité des communications pour protéger les données lors de leur transfert entre différents emplacements. Bien qu'il ait de nombreuses applications, la plupart des utilisateurs rencontrent SSL lors de la sécurisation d'une connexion Web entre une machine cliente et un serveur Web, par exemple, lors d'un achat dans une boutique en ligne.
SSL nécessite un protocole de transport sous-jacent fiable, d'où sa pertinence pour les applications sur Internet fonctionnant sur le protocole TCP (Transmission Control Protocol). Contrairement à de nombreuses autres applications de cryptographie, le déploiement de SSL est souvent rendu évident pour un utilisateur. Lors de la sécurisation des sessions Web, une connexion SSL peut être indiquée par :
• une boîte de dialogue invitant l'utilisateur à s'engager dans une « connexion sécurisée » ;
• l'apparition d'une icône, comme un cadenas, sur le navigateur Web ;
• le remplacement de http par https dans l'adresse web affichée par le navigateur.
Cryptographie pour les réseaux locaux sans fil.
Le développement de la cryptographie utilisée dans les normes de réseau local sans fil fournit un certain nombre de leçons importantes dans la conception cryptographique pratique, il fournit un bon exemple d’une technologie qui rend la cryptographie à clé publique largement disponible pour utilisation par d’autres applications.
Cryptographie pour les utilisateurs à domicile
L'une des applications concerne l’utilisation potentielle de cryptographie pour sécuriser les applications quotidiennes des particuliers telles que les fichiers cryptés, chiffrement de disque et sécurité de la messagerie.
Cryptographie pour les télécommunications mobiles
GSM et UMTS fournissent de bons exemples de conception cryptographique dans une application relativement fermée environnements.
Cryptographie pour des transactions sécurisées par carte de paiement
Le secteur bancaire est l’un des utilisateurs commerciaux les plus anciens de la cryptographie et une grande variété de différentes techniques sont utilisées pour prendre en charge différents types de transactions de paiement.
Cryptography for identity cards
Le Belgian eID card fournit un bon exemple d’une technologie qui rend la cryptographie à clé publique largement disponible pour utilisation par d’autres applications.
Cryptographie pour la diffusion vidéo
La télévision payante offre une application fascinante avec une cryptographie relativement simple nécessitant un support de gestion sophistiquée des clés.
Bibliographie
➤ James S. Kraft and Lawrence C. Washington, Textbook in mathematics "An Introduction to Number Theory with Cryptography" Second Edition CRC Press➤ Oystein Ore, Revised and Updated by John J. Watkins and Robin Wilson, "Invitation to Number Theory" Published and Distributed by The Mathematical Association of America (MAA)
➤Douglas R. Stinson and Maura B. Paterson, Textbook in mathematics "Cryptography" CRC Press
➤ Chuck Easttom, "Modern cryptography" Applied Mathematics for Encryption and Information Security, MC Graw Hill Education
➤ KEITH M. MARTIN Professor of Information Security Information Security Group, Royal Holloway, University of London "Everyday Cryptography" Fundamental Principles and Applications, OXFORD University Press 2012
➤ Czesław Kościelny · Mirosław Kurkowski Marian Srebrny, "Modern Cryptography Primer" Theoretical Foundations and Practical Applications, Springer
Autres articles
Fonction logarithme népérien
Etude de fonctions
Cryptographie
Probabilité conditionnelle
Identité de Bezout
Divisibilité dans ℤ
Le triangle de Pascal
Les nombres de Mersenne
Théorie des situations
Evaluation du travail de l'élève
Les théories de l'apprentissage
Eléments de logique mathématiques
Fractales (Partie I) - Arbres fractales
Fractales (Partie II) - Plantes fractales
Fractales (Partie III) - Courbes et formes fractales
Fractales (Partie IV) - Ensemble de Mandelbrot
MathJax - Beautiful math in all browsers
Dénombrement
Droite dans le plan
Etude de fonctions
Cryptographie
Probabilité conditionnelle
Identité de Bezout
Divisibilité dans ℤ
Le triangle de Pascal
Les nombres de Mersenne
Théorie des situations
Evaluation du travail de l'élève
Les théories de l'apprentissage
Eléments de logique mathématiques
Fractales (Partie I) - Arbres fractales
Fractales (Partie II) - Plantes fractales
Fractales (Partie III) - Courbes et formes fractales
Fractales (Partie IV) - Ensemble de Mandelbrot
MathJax - Beautiful math in all browsers
Dénombrement
Droite dans le plan
Connectez vous pour ajouter des commentaires.