Calcul dans IR : Exercice 13 2ème année secondaire
Calcul dans IRProblèmes du 1er et du second degréNotion de polynômesArithmetiqueCalcul vectorielBarycentreTranslationsHomothetiesRotationsSuitesFonctionsTrigonométrieGéométrie analytiqueGéométrie dans l'espaceStatistiquesQCM
78 exercices
Exercice 13 --- (id : 771)
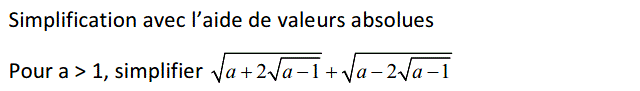
correction
Posons $X=a+2\sqrt{a-1}$ et $Y=a-2\sqrt{a-1}$
$(\sqrt X+\sqrt Y)^2$ $=X+2\sqrt X\sqrt Y+Y$
$=a+2\sqrt{a-1}$ $+2\sqrt{(a+2\sqrt{a-1})(a-2\sqrt{a-1})}$ $+a-2\sqrt{a-1}$ $=2a+2\sqrt{a^2-4(a-1)}$
$=2a+2\sqrt{a^2-4a+4}$ $=2a+2\sqrt{(a-2)^2}$ $=2a+2|a-2|$
Et puisque $\sqrt X+\sqrt Y>0$
Alors $\sqrt X+\sqrt Y=\sqrt{2a+2|a-2|}$
Autrement:
$a+2\sqrt{a-1}=(a-1)+2\sqrt{a-1}+1$ $=\sqrt{a-1}^2+2\sqrt{a-1}+1$ $=(\sqrt{a-1}+1)^2$
Et de même $a-2\sqrt{a-1}=(\sqrt{a-1}-1)^2$
Donc $\sqrt X+\sqrt Y$ $=\sqrt{a-1}+1+|\sqrt{a-1}-1|$
$(\sqrt X+\sqrt Y)^2$ $=X+2\sqrt X\sqrt Y+Y$
$=a+2\sqrt{a-1}$ $+2\sqrt{(a+2\sqrt{a-1})(a-2\sqrt{a-1})}$ $+a-2\sqrt{a-1}$ $=2a+2\sqrt{a^2-4(a-1)}$
$=2a+2\sqrt{a^2-4a+4}$ $=2a+2\sqrt{(a-2)^2}$ $=2a+2|a-2|$
Et puisque $\sqrt X+\sqrt Y>0$
Alors $\sqrt X+\sqrt Y=\sqrt{2a+2|a-2|}$
Autrement:
$a+2\sqrt{a-1}=(a-1)+2\sqrt{a-1}+1$ $=\sqrt{a-1}^2+2\sqrt{a-1}+1$ $=(\sqrt{a-1}+1)^2$
Et de même $a-2\sqrt{a-1}=(\sqrt{a-1}-1)^2$
Donc $\sqrt X+\sqrt Y$ $=\sqrt{a-1}+1+|\sqrt{a-1}-1|$
Remarque
$\sqrt X+\sqrt Y=2\sqrt{a-1}$ si $a\geqslant 2$ et $\sqrt X+\sqrt Y=2$ si $1 < a\leqslant 2$