Dénombrement
Créé par Dhaouadi Nejib le 15/01/2019
I- Revenons sur les ensembles
Un ensemble est une collection ou un groupement d'objets distincts ; ces objets s'appellent les éléments de cet ensemble.
Pour traduire q'un objet x est un élément d'un ensemble noté E, on dit que x appartient à E et on note $ x \in E$ et si x n'est pas un élément de E ou encore x n'appartient pas à E on note $x \notin E$.
- Un ensemble est fini s'il contient un nombre fini d'éléments.
- Un ensemble E est dit vide s'il ne contient aucun élément on le note $ \emptyset $.
- Un ensemble E est inclu dans un ensemble F si tout élément de E est un élément de F, on note $E \subset F$ et on dit que E est un sous-ensemble de F ou encore E est une partie de F.
- Deux ensembles E et F sont égaux si et seulement si $E \subset F$ et $F \subset E$.
L'intersection de deux ensembles E et F est l'ensemble des éléments qui appartiennent à la fois à E et à F, on le note $E \cap F$
(lire « E inter F »)
c'est-à-dire que :
$x \in E \cap F$ si et seulement si $x \in E$ et $x \in F$
Si $E \cap F=\emptyset $ on dit que les ensembles E et F sont disjoints.
c'est-à-dire que :
$x \in E \cap F$ si et seulement si $x \in E$ et $x \in F$
Si $E \cap F=\emptyset $ on dit que les ensembles E et F sont disjoints.
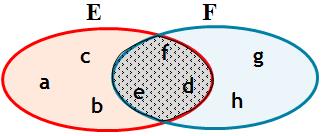 $$E \cap F=\left\{{d,e,f}\right\}$$
$$E \cap F=\left\{{d,e,f}\right\}$$
La réunion de deux ensembles E et F est l'ensemble des éléments qui appartiennent à E ou à F, on le note $E \cup F$ (lire « E union F »)
c'est-à-dire que :
$x \in E \cup F$ si et seulement si $x \in E$ ou $x \in F$
c'est-à-dire que :
$x \in E \cup F$ si et seulement si $x \in E$ ou $x \in F$
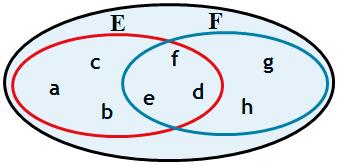 $$E \cup F=\left\{{a,b,c,d,e,f,g,h}\right\}$$
$$E \cup F=\left\{{a,b,c,d,e,f,g,h}\right\}$$
Soit E un ensemble et A un sous ensemble de E.
Le complémentaire de A dans E noté ${\complement}_{E}^{A} $ ou $\overline{A}$ est l'ensemble des éléments de E n'appartenant pas à A. c'est-à-dire que :
$x \in \overline{A}$ si et seulement si $x \in E \;et\; x \notin A$
Il est évident que $ A \cup \overline{A}=E$ et $A \cap \overline{A}=\emptyset $ on dit que A et $\overline{A}$ forment une partition de E.
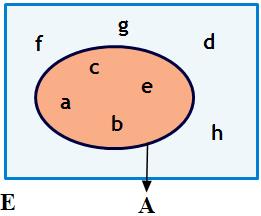
Dans l'exemple ci-contre: $\overline{A}=\left\{{d,f,g,h}\right\} $
Le complémentaire de A dans E noté ${\complement}_{E}^{A} $ ou $\overline{A}$ est l'ensemble des éléments de E n'appartenant pas à A. c'est-à-dire que :
$x \in \overline{A}$ si et seulement si $x \in E \;et\; x \notin A$
Il est évident que $ A \cup \overline{A}=E$ et $A \cap \overline{A}=\emptyset $ on dit que A et $\overline{A}$ forment une partition de E.
Dans l'exemple ci-contre: $\overline{A}=\left\{{d,f,g,h}\right\} $
La différence ensembliste de E et F notée « E \ F » (lire « E moins F ») est l'ensemble des éléments de E qui n'appartiennent pas à F, autrement dit c'est le complémentaire de F dans E, soit :
$E \backslash F=\left\{{x \in E \;| \; x \notin F}\right\}$
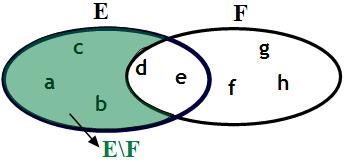 $$E \backslash F=\left\{{a,b,c}\right\}$$
$$E \backslash F=\left\{{a,b,c}\right\}$$
La différence symétrique de deux ensembles E et F est l'ensemble des éléments qui appartiennent à l'un ou l'autre des deux ensembles et non aux deux.
Cet ensemble est noté $E \, \Delta \, F$ on lit «E delta F »
ainsi : $E \, \Delta \, F=(E \backslash F) \cup (F \backslash E)$
Cet ensemble est noté $E \, \Delta \, F$ on lit «E delta F »
ainsi : $E \, \Delta \, F=(E \backslash F) \cup (F \backslash E)$
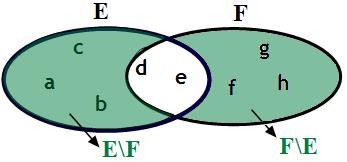 $$E \, \Delta \, F=\left\{{a,b,c,f,g,h}\right\}$$
$$E \, \Delta \, F=\left\{{a,b,c,f,g,h}\right\}$$
Formules de Morgan
Soient E un ensemble et A et B deux sous-ensembles de E
$\overline{\overline{A}}=A$ , $\overline{A \cap B}=\overline{A} \cup \overline{B}$ , $\overline{A \cup B}=\overline{A} \cap \overline{B}$
$\overline{\overline{A}}=A$ , $\overline{A \cap B}=\overline{A} \cup \overline{B}$ , $\overline{A \cup B}=\overline{A} \cap \overline{B}$
☛Définition
Soit E un ensemble fini
On appelle cardinal de E le nombre des éléments de E.
Si l'ensemble E contient n éléments, on écrit Card E=n
On appelle cardinal de E le nombre des éléments de E.
Si l'ensemble E contient n éléments, on écrit Card E=n
☛
Propriétés
E et F sont deux ensembles finis.
- $Card(E \cup F)=Card(E)+Card(F)$ $-Card(E\cap F)$
- Si E et F sont disjoints ($E\cap F=\emptyset$) on obtient :
$Card(E \cup F)=Card(E)+Card(F)$ - Si A est un sous-ensemble de E et $\overline{A}$ le complémentaire de A dans E alors: $Card(\overline{A})=Card(E)-Card(A)$
- $Card(E \backslash F)=Card(E)-Card(E \cap F)$
III-Produit cartésien de deux ensembles finis
☛Définition
Le produit cartésien (ou ensemble-produit) d'un ensemble E par un ensemble F est l'ensemble des couples dont l'origine est un élément de E et l'extrémité est un élément de F.
On le note E✕F (on lit «E crois F»)
$E\times F =\left\{{(x,y)\;tq\;\; x\in E \; et \; y \in F}\right\}$ et on a : $Card(E\times F)=Card(E)\times Card(F).$
On le note E✕F (on lit «E crois F»)
$E\times F =\left\{{(x,y)\;tq\;\; x\in E \; et \; y \in F}\right\}$ et on a : $Card(E\times F)=Card(E)\times Card(F).$
Remarques
Soit E un ensemble non vide.On sait que chaque élément du produit cartésien $E \times E$ (noté $E^2$) est un couple.
Aussi, chaque élément du produit cartésien $E \times E \times E$ (noté $E^3$) est un triplet.
Plus généralement, p étant un entier superieur ou égal à 2. Chaque élément du produit cartésien $ \underbrace{E \times E \times ... \times E}_{p fois}$ (noté $E^p$) est appelé un p-uplet
Et on a: card(E2)=(card(E))2 ; card(E3)=(card(E))3 et plus généralement card(Ep)=(card(E))p où p est un entier $\geqslant 2$
Exemple
On se propose de déterminer le nombre des entiers naturels de trois chiffres qu'on peut former à l'aide des chiffres 1,2 et 3.Pour accomplir cette tâche, il est légitime de s'aider d'un diagramme qui nous facilite la tâche. Remarquer le diagramme suivant:
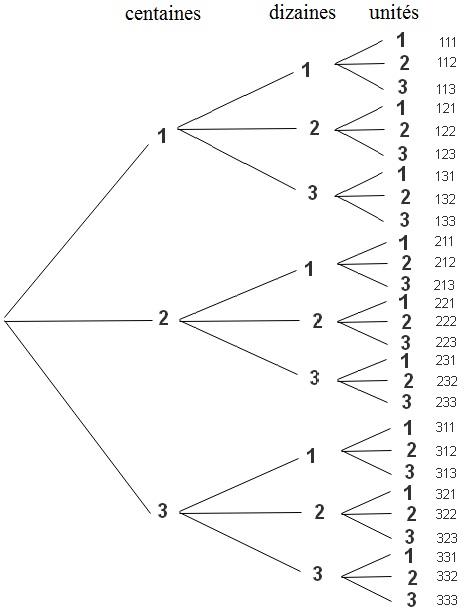
D'après le diagramme ainsi construit (appelé arbre de choix), il y a $3 \times 3 \times 3=27$ entiers obtenus.
Pour former un entier naturel de 3 chiffres, on commence par choisir le chiffre des centaines parmi les 3 choix possibles 1, 2 ou 3 et de même pour le chiffre des dizaines et le chiffre des unités ce qui revient à former un triplet dont les composants sont 1, 2 ou 3.
Donc un tel entier naturel est un élément du produit cartésien $\left\{{1,2,3}\right\} \times \left\{{1,2,3}\right\} \times \left\{{1,2,3}\right\} =\left\{{1,2,3}\right\}^3$ dont le cardinal égal à $3^3=27$.
Exercice 1
En informatique un "bit" (binary digit) vaut soit 0 soit 1, un "octet" est une succession de
huit bits (exemple : 00011001).
1. Combien existe-t-il d’octets possibles ?
2. Combien existe-t-il d’octets possibles commençant par 1 ?
3. Combien existe-t-il d’octets possibles commençant par 0 ?
4. Combien existe-t-il d’octets possibles commençant par 00 ?
1. Combien existe-t-il d’octets possibles ?
2. Combien existe-t-il d’octets possibles commençant par 1 ?
3. Combien existe-t-il d’octets possibles commençant par 0 ?
4. Combien existe-t-il d’octets possibles commençant par 00 ?
Cliquer ici pour montrer les solutions
Exercice 2
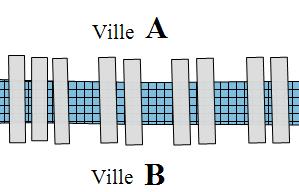
Déterminer le nombre de chemins possibles permettant d'aller de la ville A vers la ville B et de retourner de A vers B sans passer par le même pont.
Cliquer ici pour montrer les solutions
Exercice 3
Un questionnaire à choix multiples, autorisant une seule réponse par question, comprend 15 questions. Pour chaque question, on propose 4 réponses possibles.
De combien de façons peut-on répondre à ce questionnaire ?
De combien de façons peut-on répondre à ce questionnaire ?
Cliquer ici pour montrer les solutions
Exercice 4
Combien peut-on former de numéros de téléphone à 8 chiffres ?
Combien peut-on former de numéros de téléphone à 8 chiffres ne comportant pas le chiffre 0 ?
Combien peut-on former de numéros de téléphone à 8 chiffres ne comportant pas le chiffre 0 ?
Cliquer ici pour montrer les solutions
IV-Les Permutations
☛Définition
Soit E un ensemble fini et non vide de cardinal n.
On appelle permutation des éléments de E tout n-uplet d'éléments distincts de E.
Une permutation de E est assimilée à une numérotation des n éléments de E de 1 jusqu'a n qu'on peut mettre en évidence simplement en écrivant ces éléments suivant l'ordre de cette numérotation.
Le nombre des permutations de E est égal à: n x (n-1) x (n-2) x ... x 2 x 1.
On appelle permutation des éléments de E tout n-uplet d'éléments distincts de E.
Une permutation de E est assimilée à une numérotation des n éléments de E de 1 jusqu'a n qu'on peut mettre en évidence simplement en écrivant ces éléments suivant l'ordre de cette numérotation.
Le nombre des permutations de E est égal à: n x (n-1) x (n-2) x ... x 2 x 1.
Notation
Soit n un entier naturel non nul.On appelle factorielle de n et on note n!, l’entier 1x 2x …x n. Par suite, le nombre des permutations des n éléments de E est égal à n! .
On convient que 0!=1.
Exercice 5
1. Calculer 4! ; 5! ; 6! ; 7! ; 8!.
2. Calculer $\frac{8!}{4!}\;,\frac{12!}{14!} \;,\; \frac{120!}{119!}\; et \; \frac{100!}{97!} $
3. Montrer que 2 x 4 x ... x 200=2100100!
4. Montrer que $\frac{2 \times 4 \times ... \times 2000}{3 \times 5 \times ... \times 2001}=\frac{{\left({2^{1000}\times 1000!}\right)}^{2}}{2001!}$
2. Calculer $\frac{8!}{4!}\;,\frac{12!}{14!} \;,\; \frac{120!}{119!}\; et \; \frac{100!}{97!} $
3. Montrer que 2 x 4 x ... x 200=2100100!
4. Montrer que $\frac{2 \times 4 \times ... \times 2000}{3 \times 5 \times ... \times 2001}=\frac{{\left({2^{1000}\times 1000!}\right)}^{2}}{2001!}$
Cliquer ici pour montrer les solutions
Exercice 6
- On appelle anagramme du mot MATH tout mot (ayant un sens ou non) formé des quatre lettres M, A, T et H.
Combien y a-t-il d’anagrammes du mot MATH ? - Combien y a-t-il d’anagrammes du mot LOGIQUE ?
- Combien y a-t-il d’anagrammes du mot TUNISIE ?
- Combien y a-t-il d’anagrammes du mot BACCALAUREAT ?
Cliquer ici pour montrer les solutions
V. Arrangement
☛Définition
Soit E un ensemble fini non vide de cardinal n et p un entier naturel tel que 1 ≤ p ≤ n.
On appelle arrangement de p éléments de E tout p-uplet d’éléments distincts de E.
Le nombre d’arrangements de p éléments de E est l’entier noté ${A}_{n}^{p}$ (on lit «A, n, p»),tel que
$${A}_{n}^{p}=n\times(n-1)\times ... \times (n-p+1)=\frac{n!}{(n-p)!} $$ On convient que ${A}_{n}^{0}=1$
Le nombre d’arrangements de p éléments de E est l’entier noté ${A}_{n}^{p}$ (on lit «A, n, p»),tel que
$${A}_{n}^{p}=n\times(n-1)\times ... \times (n-p+1)=\frac{n!}{(n-p)!} $$ On convient que ${A}_{n}^{0}=1$
Exemple
Soit l'ensemble $E=\left\{{a,b,c,d}\right\}$Un arrangement de trois éléments de E est un triplet d'éléments distincts de E.
On peut citer, par exemple:(a,b,c),(a,b,d),(d,a,c),(d,a,b),(d,b,a) etc ...
Le nombre des triplets possibles est égal à ${A}_{4}^{3}=4 \times 3 \times 2=24$.
Exercice 7
On considère une course à laquelle participent dix athlètes.
Combien existe-t-il d'ordres d'arrivées possibles des trois premiers (sans ex-æquo)?
Combien existe-t-il d'ordres d'arrivées possibles des trois premiers (sans ex-æquo)?
Cliquer ici pour montrer les solutions
Exercice 8
A l'aide des chiffres de 1 à 7
- Combien peut-on former de nombre de quatre chiffres?
- Combien peut-on former de nombre de quatre chiffres distincts?
- Reprendre les deux questions précédentes à l'aide des chiffres de 0 à 7.
Cliquer ici pour montrer les solutions
VI. Combinaisons
☛Définition
Soit E un ensemble fini non vide de cardinal n et p un entier naturel tel que $0\leqslant p\leqslant n$.
On appelle combinaison de p éléments de E, toute partie de p éléments distincts de E.
Le nombre de parties à p éléments d'un ensemble de n éléments est noté ${C}_{n}^{p}$ ou $\left({\begin{aligned}&{n}\\&{p}\end{aligned}}\right)$
Soit n et p deux entiers naturels tels que n ≥ 1 et 0 ≤ p ≤ n.On appelle combinaison de p éléments de E, toute partie de p éléments distincts de E.
Le nombre de parties à p éléments d'un ensemble de n éléments est noté ${C}_{n}^{p}$ ou $\left({\begin{aligned}&{n}\\&{p}\end{aligned}}\right)$
Pour former tous les arrangements de p éléments de E, on applique à chaque partie de p éléments de E toutes les p! permutations possibles, ce qui permet de dire que ${A}_{n}^{p}=p!{C}_{n}^{p}$ ou encore: $$ \boxed{{C}_{n}^{p}=\frac{n!}{p!(n-p)!}} $$
☛
Propriétés
- L'ensemble vide $\emptyset$ qui contient 0 élément, admet une seule partie de 0 élément qui est $\emptyset$ (lui même) donc ${C}_{0}^{0}=1$
- L'ensemble vide $\emptyset$ est toujour la seule partie de n'importe quel ensemble de n éléments, qui contient 0 élément donc ${C}_{n}^{0}=1$
- A l'aide des n éléments d'un ensemble ($n \geqslant 1 $), on peut former exactement n parties contenant chacune un seul élément (appelées des singletons) donc ${C}_{n}^{1}=n$
- Dans un ensemble E de n éléments ($n \geqslant 1$), le choix d'un singleton correspond exactement au choix d'une partie de n-1 éléments (Les éléments de E autre que l'élément du singleton) donc ${C}_{n}^{n-1}={C}_{n}^{1}=n$
- Soit E un ensemble de cardinal n et p tel que 0 ≤ p ≤ n. Choisir une partie à p éléments de E revient à choisir une partie à n – p éléments. donc ${C}_{n}^{p}={C}_{n}^{n-p}$
- Il y a deux façons de choisir p éléments parmi n éléments
➽ soit on prend un élément bien précis désigné à l'avance et il reste p-1 éléments parmi n-1 éléments, ce qui fait ${C}_{n-1}^{p-1}$ possibilités
➽ soit on ne prend pas cet élément et il faut choisir p éléments parmi n-1 éléments, ce qui fait ${C}_{n-1}^{p}$ possibilités.
D'où l'égalité :$$ {C}_{n}^{p}={C}_{n-1}^{p-1}+{C}_{n-1}^{p}$$
Exercice 9
Une urne contient trois boules blanches et cinq boules noires.
On tire simultanément quatre boules de l’urne.
On tire simultanément quatre boules de l’urne.
- Combien y a-t-il de tirages possibles ?
- Combien y a-t-il de tirages qui contiennent une seule boule blanche ?
- Combien y a-t-il de tirages qui contiennent deux boules blanches ?
- Combien y a-t-il de tirages qui contiennent trois boules blanches ?
- Combien y a-t-il de tirages qui contiennent quatre boules blanches ?
- Combien y a-t-il de tirages qui contiennent au moins une boule blanche ?
Cliquer ici pour montrer les solutions
Exercice 10
On constitue un groupe de 6 personnes choisies parmi 25 femmes et 32 hommes.
- De combien de façons peut-on constituer ce groupe de 6 personnes ?
- Dans chacun des cas suivants, de combien de façons peut-on constituer ce groupe avec :
a) uniquement des hommes.
b) des personnes de même sexe.
c) au moins une femme et au moins un homme.
Cliquer ici pour montrer les solutions
VII. Triangle de Pascal et binôme de Newton
Triangle de Pascal
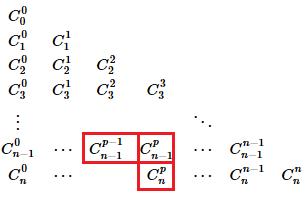
Et d'après la dernière propriété plus haut, le triangle de pascal deient très simple à établir.
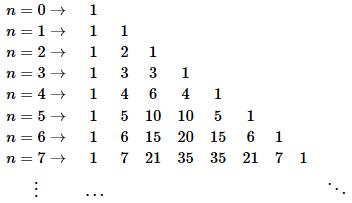

Nombre de parties d'un ensemble fini.
Dans la formule du binôme, pour a=1 et b=1 on obtient:$2^n={C}_{n}^{0}+{C}_{n}^{1}+ \dots +{C}_{n}^{n}$
Chacun des nombres ${C}_{n}^{p}$ représente le nombre de parties de p éléments d'un ensemble de n éléments ($0 \leqslant p \leqslant n$)
D'où le théorème suivant:
☛
Théorème
Le nombre de parties d'un ensemble de n éléments est égal à $2^n$
VIII. Autres exercices
Exercice 1
A l'aide des chiffres 2, 3, 4, 5, 6, 7, combien peut-on écrire:
- de nombres de trois chiffres?
- de nombres de trois chiffres distincts?
- de nombres de six chiffres?
- de nombres de six chiffres distincts?
Exercice 2
Un sac contient cinq jetons blancs et quatre jetons noirs.
On prend simultanément trois jetons du sac.
De combient de façons peut-on ainsi extraire:
On prend simultanément trois jetons du sac.
De combient de façons peut-on ainsi extraire:
- Un jeton noir et un seulement?
- Un jeton blanc et un seulement?
- Trois jetons noirs?
- Aucun jeton noir?
- Au moins deux jetons blancs?
- Au plus deux jetons blancs?
Exercice 3
Trois dés de couleurs differentes ont des faces numérotées de 1 à 6.
On jette ces trois dés et on observe les nombres inscrits sur les faces superieures.
On jette ces trois dés et on observe les nombres inscrits sur les faces superieures.
- Dénombrer tous les résultats possibles.
- Dénombrer les résultats comportant un seul 3.
- Dénombrer les résultats comportant exactement deux 4.
- Dénombrer les résultats ne comportant aucune 5.
Exercice 4
Une assemblée de dix hommes et huit femmes désirent élire un comité de cinq membres.
Madame A et Monsieur B ne peuvent pas faire partie d'un même comité.
Madame A et Monsieur B ne peuvent pas faire partie d'un même comité.
- Quel est le nombre de comités dont Madame A ferait partie?
- Quel est, dans les conditions précisées par les énoncés, le nombre de comités qui pourraient être constitués?
Exercice 5
- De combien de façons peut-on placer 5 boules de couleurs différentes dans 5 boites alignées? (on place une boule dans chaque boite)
- De combien de façons peut-on placer 5 boules à choisir parmi 12 boules de couleurs différentes, dans 5 boites alignées?
- De combien de façons peut-on placer 5 boules à choisir parmi 7 boules blanches et 10 boules noires, dans 5 boites alignées?
- De combien de façons peut-on placer 7 boules blanches et 10 boules noires dans 20 boites alignées?
Exercice 6
On constitue une file d’attente en attribuant au hasard des numéros d’ordre à n personnes ($n\geqslant 2$). Deux amis A et B se trouvent dans cette file d’attente.
- Dénombrer le nombre de façons où les deux amis soient situés l’un derrière l’autre ?
- Dénombrer le nombre de façons où les deux amis soient distants de p places (i.e. séparés par p − 1 personnes) ?
Cliquer ici pour montrer les solutions
Autres articles
Fonction logarithme népérien
Etude de fonctions
Cryptographie
Probabilité conditionnelle
Identité de Bezout
Divisibilité dans ℤ
Le triangle de Pascal
Les nombres de Mersenne
Théorie des situations
Evaluation du travail de l'élève
Les théories de l'apprentissage
Eléments de logique mathématiques
Fractales (Partie I) - Arbres fractales
Fractales (Partie II) - Plantes fractales
Fractales (Partie III) - Courbes et formes fractales
Fractales (Partie IV) - Ensemble de Mandelbrot
MathJax - Beautiful math in all browsers
Dénombrement
Droite dans le plan
Etude de fonctions
Cryptographie
Probabilité conditionnelle
Identité de Bezout
Divisibilité dans ℤ
Le triangle de Pascal
Les nombres de Mersenne
Théorie des situations
Evaluation du travail de l'élève
Les théories de l'apprentissage
Eléments de logique mathématiques
Fractales (Partie I) - Arbres fractales
Fractales (Partie II) - Plantes fractales
Fractales (Partie III) - Courbes et formes fractales
Fractales (Partie IV) - Ensemble de Mandelbrot
MathJax - Beautiful math in all browsers
Dénombrement
Droite dans le plan
Dhaouadi Nejib01-04-2021 19:57:58
Ce cours en pdf
recopier et coller ce lien dans la zone des adresses en haut de la bage:
https://www.sigmaths.net/up_docs/details.php?doc_id=376
recopier et coller ce lien dans la zone des adresses en haut de la bage:
https://www.sigmaths.net/up_docs/details.php?doc_id=376
Thimbo Abdoulaye01-04-2021 19:46:45
Mashallah ! C'est très intéressant. Mais comment faire pour le télécharger en format PDF ?
Connectez vous pour ajouter des commentaires.
Commentaires