Arbres fractales

L'adjectif « fractal », à partir duquel l'usage a imposé le substantif une fractale pour désigner une figure ou une équation de géométrie fractale, est un néologisme créé par Benoît Mandelbrot en 1974 à partir de la racine latine fractus, qui signifie « brisé », « irrégulier », et de la désinence -al présente dans les adjectifs naval et banal (pluriels : navals, banals, fractals). De nombreux phénomènes naturels – comme le tracé des lignes de côtes ou l'aspect du chou romanesco – possèdent des formes fractales approximatives.
Les fractales sont définies de manière paradoxale, à l'image des poupées russes qui renferment une figurine identique à l'échelle près : « les objets fractals peuvent être envisagés comme des structures gigognes en tout point et pas seulement en un certain nombre de points, les attracteurs de la structure gigogne classique. Cette conception hologigogne (gigogne en tout point) des fractales implique cette définition tautologique : un objet fractal est un objet dont chaque élément est aussi un objet fractal (similaire).
Les fractales sont des objets, qu’ils soient mathématiques, dus à la nature ou dus à l’homme, qu’on appelle irréguliers, rugueux, poreux ou fragmentés, et qui, de plus, possèdent ces propriétés au même degré à toutes les échelles. C’est dire que ces objets ont la même forme, qu’ils soient vus de près ou de loin.

La dimension d'une ligne droite, d'un cercle et d'une courbe régulière est de 1. La dimension d'une figure simple dans le plan est de 2. La dimension d'un corps simple dans l'espace est de 3.
Une figure telle qu'une fractale n'est pas simple. Sa dimension n'est plus aussi facile à définir et n'est plus forcément entière. La dimension fractale, plus complexe, s'exprime à l'aide de la dimension de Hausdorff.
Quand la fractale est formée de répliques d'elle-même en plus petit, sa dimension fractale peut se calculer comme suit $$ d=\frac {ln(n)}{ln(h)}$$ où la fractale de départ est formée de $n$ exemplaires dont la taille a été réduite d'un facteur $h$ (pour homothétie).

Des formes fractales approximatives sont facilement observables dans la nature. La théorie mathématique des fractales peut apporter des informations intéressantes dans plusieurs domaines scientifiques comme :

• en géologie, étude du relief, côtes et cours d'eau, structures de roches, avalanches.
• en morphologie animale, structures des Invertébrés, plumes d'oiseaux
• en médecine, structure des poumons, intestins, battements du cœur.
• en météorologie, nuages, vortex, banquise, vagues scélérates, turbulences, structure de la foudre.
• en volcanologie, prévision d'éruptions volcaniques, tremblements de terre.
• en astronomie avec la description des structures de l'univers, cratères sur la Lune, répartition des galaxies.
• en sciences humaines, structure urbaine, évolution de la démographie.

Les arbres botaniques sont des fractales et il existe aussi des arbres dans le corps humain, dans les poumons (on parle de l'arbre bronchique), et dans le système artériel.

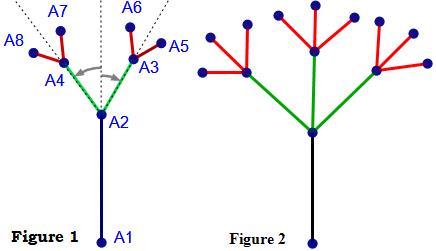
La figure "Figure1" shématise la branche d'un arbre qui se subdivise en deux branches, chacune d'elle pouvant se subdiviser à son tour en deux branches etc..
Les segments $[A_2A_3]$ et $[A_2A_4]$ sont les images du segment $[A_1A_2]$ par deux similitudes directes de même centre $A_2$ de même rapport $k \in \left]{0,1}\right[$ et d'angles $\alpha>0$ et $\beta <0$. Les segments $[A_3A_5]$ et $[A_3A_6]$ sont les images du segment $[A_2A_3]$ par deux similitudes directes de même centre $A_3$ de rapport $k$ et d'angles $\alpha$ et $\beta$ etc ...
Si on note $K_0=[A_1A_2]$ et $K_1=[A_2A_3]\cup[A_2A_4]$ et $K_2=[A_3A_5]\cup [A_3A_6]\cup[A_4A_7]\cup[A_4A_8]$ etc ... alors l'arbre fractal obtenu après n itérations est $\bigcup_{i=1}^{n}{K_i}$
De la même façon, on peut modéliser un arbre fractal comme dans la figure 2.