Calcul dans IR : Exercice 6 2ème année secondaire
Calcul dans IRProblèmes du 1er et du second degréNotion de polynômesArithmetiqueCalcul vectorielBarycentreTranslationsHomothetiesRotationsSuitesFonctionsTrigonométrieGéométrie analytiqueGéométrie dans l'espaceStatistiquesQCM
78 exercices
Exercice 6 --- (id : 109)
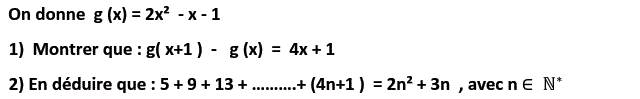
correction
1)
$$\begin{align*}
&g(x+1)-g(x)\\
&=[2(x+1)^2-(x+1)-1]-(2x^2-x-1)\\
&=[2(x^2+2x+1)-(x+1)-1]-(2x^2-x-1) \\
&=(2x^2+4x+2-x-1-1)-(2x^2-x-1) \\
&=2x^2+4x+2-x-2-2x^2+x+1 \\
&=4x+1
\end{align*}$$
2)
On a : $g(x+1)-g(x)=4x+1$ pour tout réel x
Pour $x=1$: $g(2)-g(1)=4\times 1+1=5$
Pour $x=2$: $g(3)-g(2)=4\times 2+1=9$
Pour $x=3$: $g(4)-g(3)=4\times 3+1=13$
.....
Pour $x=n$: $g(n+1)-g(n)=4n+1$
Donc on peut écrire :
$3+9+13+...+(4n+1)$
$=g(2)-g(1)$ $+g(3)-g(2)$ $+g(4)-g(3)+...$ $+g(n+1)-g(n)$
Après simplification on obtient:
$3+9+13+...+(4n+1)$ $=g(n+1)-g(1)$
$=[2(n^2+2n+1)-(n+1)-1]-0$
$=2n^2+4n+2-n-1-1$
$=2n^2+3n$
Pour $x=1$: $g(2)-g(1)=4\times 1+1=5$
Pour $x=2$: $g(3)-g(2)=4\times 2+1=9$
Pour $x=3$: $g(4)-g(3)=4\times 3+1=13$
.....
Pour $x=n$: $g(n+1)-g(n)=4n+1$
Donc on peut écrire :
$3+9+13+...+(4n+1)$
$=g(2)-g(1)$ $+g(3)-g(2)$ $+g(4)-g(3)+...$ $+g(n+1)-g(n)$
Après simplification on obtient:
$3+9+13+...+(4n+1)$ $=g(n+1)-g(1)$
$=[2(n^2+2n+1)-(n+1)-1]-0$
$=2n^2+4n+2-n-1-1$
$=2n^2+3n$