Calcul dans IR : Exercice 5 2ème année secondaire
Calcul dans IRProblèmes du 1er et du second degréNotion de polynômesArithmetiqueCalcul vectorielBarycentreTranslationsHomothetiesRotationsSuitesFonctionsTrigonométrieGéométrie analytiqueGéométrie dans l'espaceStatistiquesQCM
78 exercices
Exercice 5 --- (id : 777)
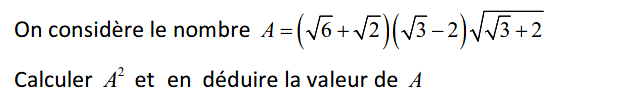
correction
$$\begin{align*}
🔷A^2&=\left[{\left({\sqrt{6}+\sqrt{2}}\right)\left({\sqrt{3}-2}\right)\left({\sqrt{\sqrt{3}+2}}\right)}\right]^2\\
&=\left({\sqrt{6}+\sqrt{2}}\right)^2\left({\sqrt{3}-2}\right)^2\sqrt{\sqrt{3}+2}^2\\
& =\left({\sqrt{6}+\sqrt{2}}\right)^2\left({2-\sqrt{3}}\right)^2\sqrt{\sqrt{3}+2}^2 \\
& =\left({6+2\sqrt{6}\sqrt{2}+2}\right)\left({2-\sqrt{3}}\right)\left({2-\sqrt{3}}\right)\left({2+\sqrt{3}}\right) \\
&=\left({8+2\sqrt{12}}\right)\left({2-\sqrt{3}}\right)\left({4-3}\right) \\
&=\left({8+4\sqrt{3}}\right)\left({2-\sqrt{3}}\right) \\
&16-8\sqrt{3}+8\sqrt{3}-12=4 \\
🔷A^2&=4\Leftrightarrow A=-2\; ou\; A=2
\end{align*}$$
Or $\sqrt{3}-2<0$ (Les deux autres facteurs sont positifs) donc $A<0$
d'où $\boxed{A=-2}$
Remarque
On peut aussi calculer directement A de la façon suivante:
$$\begin{align*}
A&=\left({\sqrt{6}+\sqrt{2}}\right)\left({\sqrt{3}-2}\right)\left({\sqrt{\sqrt{3}+2}}\right)\\
&=\sqrt{2}\left({\sqrt{3}+1}\right)\left({\sqrt{3}-2}\right)\sqrt{\sqrt{3}+2}\\
&=-\left({\sqrt{3}+1}\right)\left({2-\sqrt{3}}\right)\sqrt{2}\sqrt{2+\sqrt{3}}\\
&=-\left({\sqrt{3}+1}\right)\left({2-\sqrt{3}}\right)\sqrt{4+2\sqrt{3}}\\
&=-\left({\sqrt{3}+1}\right)\left({2-\sqrt{3}}\right)\sqrt{\left({\sqrt{3}+1}\right)^2}\\
&=-\left({\sqrt{3}+1}\right)^2\left({2-\sqrt{3}}\right)\\
&=-\left({4+2\sqrt{3}}\right)\left({2-\sqrt{3}}\right)\\
&=-2\left({2+\sqrt{3}}\right)\left({2-\sqrt{3}}\right)\\
&=-2\left({4-3}\right)=-2
\end{align*}$$