Problèmes du 1er et du second degré : Exercice 9 2ème année secondaire
Calcul dans IRProblèmes du 1er et du second degréNotion de polynômesArithmetiqueCalcul vectorielBarycentreTranslationsHomothetiesRotationsSuitesFonctionsTrigonométrieGéométrie analytiqueGéométrie dans l'espaceStatistiquesQCM
115 exercices
Exercice 9 --- (id : 11)
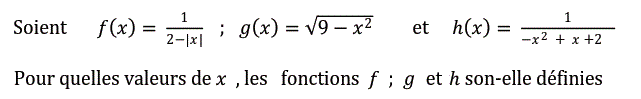
correction
🟩$f(x)$ existe $\Leftrightarrow 2-|x|\neq 0 $ $\Leftrightarrow |x|\neq 2$ $\Leftrightarrow x\neq 2$ et $x\neq -2$
Donc $D_f=\Bbb R ╲\left\{{-2,2}\right\}$
🟩$g(x)$ existe $\Leftrightarrow 9-x^2\geqslant 0$ $\Leftrightarrow x\in \left]{-\infty,-3}\right]\cup\left[{3,+\infty}\right[$
Donc $D_g=\left]{-\infty,-3}\right]\cup\left[{3,+\infty}\right[$
🟩$h(x)$ existe $\Leftrightarrow -x^2+x+2\neq 0$
$\Delta=b^2-4ac$ $=1-4\times (-1)\times 2=9 $ donc $x'=\frac{-1-3}{-2}=2$ et $x''=\frac{-1+3}{-2}=-1$
Alors $D_h=\Bbb R╲\left\{{-1,2}\right\}$
Donc $D_f=\Bbb R ╲\left\{{-2,2}\right\}$
🟩$g(x)$ existe $\Leftrightarrow 9-x^2\geqslant 0$ $\Leftrightarrow x\in \left]{-\infty,-3}\right]\cup\left[{3,+\infty}\right[$
Donc $D_g=\left]{-\infty,-3}\right]\cup\left[{3,+\infty}\right[$
🟩$h(x)$ existe $\Leftrightarrow -x^2+x+2\neq 0$
$\Delta=b^2-4ac$ $=1-4\times (-1)\times 2=9 $ donc $x'=\frac{-1-3}{-2}=2$ et $x''=\frac{-1+3}{-2}=-1$
Alors $D_h=\Bbb R╲\left\{{-1,2}\right\}$