Suites : Exercice 8 2ème année secondaire
Calcul dans IRProblèmes du 1er et du second degréNotion de polynômesArithmetiqueCalcul vectorielBarycentreTranslationsHomothetiesRotationsSuitesFonctionsTrigonométrieGéométrie analytiqueGéométrie dans l'espaceStatistiquesQCM
86 exercices
Exercice 8 --- (id : 956)
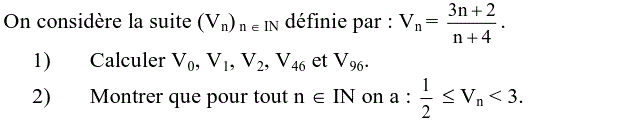
correction
$V_n=\dfrac{3n+2}{n+4}$
1
🔹$V_0=\dfrac{2}{4}=\dfrac{1}{2}$
🔹$V_1=\dfrac{3+2}{1+4}=1$
🔹$V_2=\dfrac{6+2}{2+4}=\dfrac{8}{6}=\dfrac{4}{3}$
🔹$V_{46}=\dfrac{3\times46+2}{46+4}=\dfrac{140}{50}=\dfrac{14}{5}=2,8$
🔹$V_{96}=\dfrac{3\times96+2}{96+4}=\dfrac{290}{100}=\dfrac{29}{10}=2,9$
🔹$V_1=\dfrac{3+2}{1+4}=1$
🔹$V_2=\dfrac{6+2}{2+4}=\dfrac{8}{6}=\dfrac{4}{3}$
🔹$V_{46}=\dfrac{3\times46+2}{46+4}=\dfrac{140}{50}=\dfrac{14}{5}=2,8$
🔹$V_{96}=\dfrac{3\times96+2}{96+4}=\dfrac{290}{100}=\dfrac{29}{10}=2,9$
2
$V_n=\dfrac{3n+2}{n+4}=\dfrac{3(n+4)-10}{n+4}=3-\dfrac{10}{n+4}$👍
$n+4\geqslant 4$ $\iff 0<\dfrac{1}{n+4}\leqslant\dfrac{1}{4}$ $\iff -\dfrac{10}{4}\leqslant -\dfrac{10}{n+4}<0$ $\iff 3-\dfrac{10}{4}\leqslant 3-\dfrac{10}{n+4}<3$ $\iff \dfrac{2}{4}\leqslant V_n<3$ $\iff \dfrac{1}{2}\leqslant V_n<3$
$n+4\geqslant 4$ $\iff 0<\dfrac{1}{n+4}\leqslant\dfrac{1}{4}$ $\iff -\dfrac{10}{4}\leqslant -\dfrac{10}{n+4}<0$ $\iff 3-\dfrac{10}{4}\leqslant 3-\dfrac{10}{n+4}<3$ $\iff \dfrac{2}{4}\leqslant V_n<3$ $\iff \dfrac{1}{2}\leqslant V_n<3$