Trigonométrie : Exercice 7 2ème année secondaire
Calcul dans IRProblèmes du 1er et du second degréNotion de polynômesArithmetiqueCalcul vectorielBarycentreTranslationsHomothetiesRotationsSuitesFonctionsTrigonométrieGéométrie analytiqueGéométrie dans l'espaceStatistiquesQCM
24 exercices
Exercice 7 --- (id : 906)
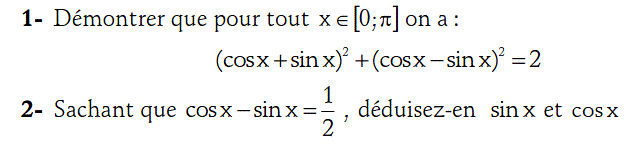
correction
1 Pour tout réel x on a :
$$\begin{align*}
&(\cos x+\sin x)^2+(\cos x -\sin x)^2 \\
&=\underbrace{\cos^2x+\sin^2x}_{=1}+\cancel{2\cos x\sin x}+\underbrace{\cos^2x+\sin^2x}_{=1}-\cancel{2\cos x\sin x}\\
&=1+1\\
&=2
\end{align*}$$
2
Pour $x\in \left[{0;\pi}\right]$, $\sin x\geqslant 0$
$\cos x-\sin x=\dfrac{1}{2}\geqslant 0$ $\Longrightarrow \cos x\geqslant \sin x\geqslant 0$ $\Longrightarrow \cos x\geqslant 0$
$(\cos x+\sin x)^2+(\cos x -\sin x)^2=2$
$\iff (\cos x+\sin x)^2+\left({\dfrac{1}{2}}\right)^2=2$
$\iff (\cos x+\sin x)^2+\dfrac{1}{4}=2$
$\iff (\cos x+\sin x)^2=2-\dfrac{1}{4}=\dfrac{7}{4}$
$\iff \cos x+\sin x=\sqrt{\dfrac{7}{4}}$ car $\cos x+\sin x\geqslant0$
$\left\{{\begin{aligned}&{\cos x+\sin x=\dfrac{\sqrt{7}}{2}}\\&{\cos x-\sin x=\dfrac{1}{2}}\end{aligned}}\right.$ $\iff \left\{{\begin{aligned}&{2\cos x=\dfrac{\sqrt{7}+1}{2}}\\&{2\sin x=\dfrac{\sqrt{7}-1}{2}}\end{aligned}}\right.$ $\iff \left\{{\begin{aligned}&{\cos x=\dfrac{\sqrt{7}+1}{4}}\\&{\sin x=\dfrac{\sqrt{7}-1}{4}}\end{aligned}}\right.$
$\cos x-\sin x=\dfrac{1}{2}\geqslant 0$ $\Longrightarrow \cos x\geqslant \sin x\geqslant 0$ $\Longrightarrow \cos x\geqslant 0$
$(\cos x+\sin x)^2+(\cos x -\sin x)^2=2$
$\iff (\cos x+\sin x)^2+\left({\dfrac{1}{2}}\right)^2=2$
$\iff (\cos x+\sin x)^2+\dfrac{1}{4}=2$
$\iff (\cos x+\sin x)^2=2-\dfrac{1}{4}=\dfrac{7}{4}$
$\iff \cos x+\sin x=\sqrt{\dfrac{7}{4}}$ car $\cos x+\sin x\geqslant0$
$\left\{{\begin{aligned}&{\cos x+\sin x=\dfrac{\sqrt{7}}{2}}\\&{\cos x-\sin x=\dfrac{1}{2}}\end{aligned}}\right.$ $\iff \left\{{\begin{aligned}&{2\cos x=\dfrac{\sqrt{7}+1}{2}}\\&{2\sin x=\dfrac{\sqrt{7}-1}{2}}\end{aligned}}\right.$ $\iff \left\{{\begin{aligned}&{\cos x=\dfrac{\sqrt{7}+1}{4}}\\&{\sin x=\dfrac{\sqrt{7}-1}{4}}\end{aligned}}\right.$