Problèmes du 1er et du second degré : Exercice 7 2ème année secondaire
Calcul dans IRProblèmes du 1er et du second degréNotion de polynômesArithmetiqueCalcul vectorielBarycentreTranslationsHomothetiesRotationsSuitesFonctionsTrigonométrieGéométrie analytiqueGéométrie dans l'espaceStatistiquesQCM
115 exercices
Exercice 7 --- (id : 8)
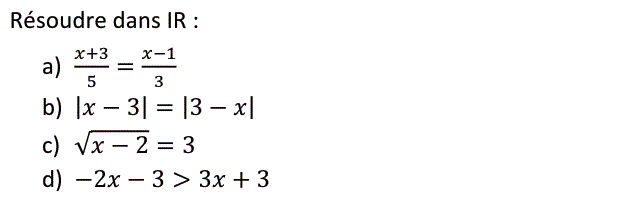
correction
On note $S_\Bbb R$ l'ensemble des solutions de l'équation (ou l'inéquation) donnée.
a)
$\dfrac{x+3}{5}=\dfrac{x-1}{3}$ $\Leftrightarrow 3(x+3)=5(x-1)$ $\Leftrightarrow 3x+9=5x-5$ $\Leftrightarrow 2x=14$ $\Leftrightarrow x=7$
Donc $\boxed{S_\Bbb R=\left\{{7}\right\}}$
Donc $\boxed{S_\Bbb R=\left\{{7}\right\}}$
b)
$\left|{x-3}\right|=\left|{3-x}\right|$ $\Leftrightarrow |x-3|=|-(x-3)|$ $\Leftrightarrow |x-3|=|x-3|$ ce qui est vrai pour tout réel x
Donc $\boxed{S_\Bbb R=\Bbb R}$
Donc $\boxed{S_\Bbb R=\Bbb R}$
c)
$\sqrt{x-2}=3$ $\Leftrightarrow x-2=3^2$ et $x-2\geqslant 0$ $\Leftrightarrow x=11$
Donc $\boxed{S_\Bbb R=\left\{{11}\right\}}$
Donc $\boxed{S_\Bbb R=\left\{{11}\right\}}$
d)
$-2x-3>3x+3$ $\Leftrightarrow -2x-3x>3+3$ $\Leftrightarrow -5x>6$ $\Leftrightarrow x<-\frac{6}{5}$
Donc $\boxed{S_\Bbb R=\left]{-\infty; -\frac{6}{5}}\right[}$
Donc $\boxed{S_\Bbb R=\left]{-\infty; -\frac{6}{5}}\right[}$