Géométrie analytique : Exercice 6 2ème année secondaire

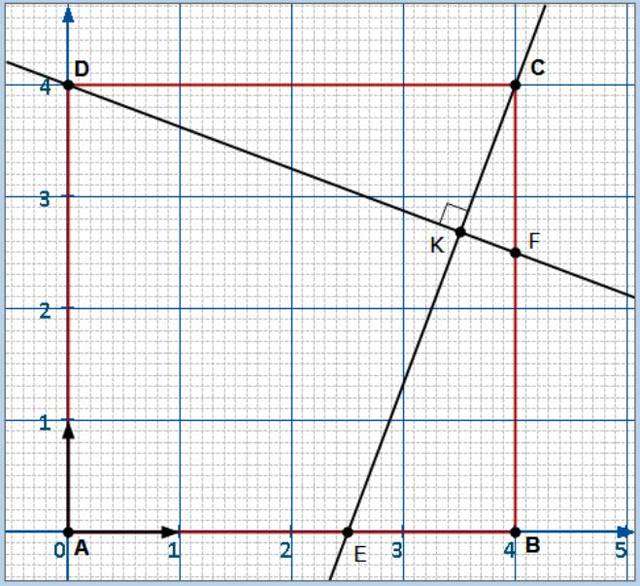
1 Considérons le repère $(O,\vec i,\vec j)$ où $\vec i=\dfrac{1}{4}\overrightarrow{AB}$ et $\vec j=\dfrac{1}{4}\overrightarrow{AD}$
Dans le repère $(O,\vec i,\vec j)$ on a : $C(4;4)$ , $E(2,5;0)$ , $D(0;4)$ et $F(4;2,5)$
🔸 $M(x;y)\in (CE)$ $\iff \overrightarrow{CM}\left({\begin{aligned}&{x-4}\\&{y-4}\end{aligned}}\right)$ et $\overrightarrow{CE}\left({\begin{aligned}&{-1,5}\\&{-4}\end{aligned}}\right)$ sont colinéaires $\iff \begin{vmatrix}{x-4}&{-1,5}\\{y-4}&{-4}\end{vmatrix}=0$ $\iff -4(x-4)+1,5(y-4)=0$ $\iff -4x+1,5y+10=0$
Donc $\boxed{(CE): -4x+1,5y+10=0}$
🔸 $M(x;y)\in (DF)\iff$ les vecteurs $\overrightarrow{DM}\left({\begin{aligned}&{x}\\&{y-4}\end{aligned}}\right)$ et $\overrightarrow{DF}\left({\begin{aligned}&{4}\\&{-1,5}\end{aligned}}\right)$ sont colinéaires $\iff \begin{vmatrix}{x}&{4}\\{y-4}&{-1,5}\end{vmatrix}=0$ $\iff -1,5x-4(y-4)=0$ $\iff -1,5x-4y+16=0$
Donc $\boxed{(DF): 1,5x+4y-16=0}$

2 $K(x;y)\in (CE)\cap (DF)$ $\iff \left\{{\begin{aligned}&{-4x+1,5y+10=0}\\&{1,5x+4y-16=0}\end{aligned}}\right.$ $\iff \left\{{\begin{aligned}&{-4x+\dfrac{3}{2}y+10=0}\\&{\dfrac{3}{2}x+4y-16=0}\end{aligned}}\right.$ $\iff \left\{{\begin{aligned}&{-8x+3y+20=0}\\&{3x+8y-32=0}\end{aligned}}\right.$ $\iff \left\{{\begin{aligned}&{-24x+9y+60=0}\\&{24x+64y-256=0}\end{aligned}}\right.$ $\iff \left\{{\begin{aligned}&{73y-196=0}\\&{3x=32-8y}\end{aligned}}\right.$ $\iff \left\{{\begin{aligned}&{y=\dfrac{196}{73}}\\&{x=\dfrac{1}{3}(32-8y)=\dfrac{256}{73}}\end{aligned}}\right.$

3 $\overrightarrow{CE}\left({\begin{aligned}&{-1,5}\\&{-4}\end{aligned}}\right)$ et $\overrightarrow{DF}\left({\begin{aligned}&{4}\\&{-1,5}\end{aligned}}\right)$
🔸 Condition d'orthogonalité : $aa'+bb'=(-1,5)\times 4+(-4)\times (-1,5)=-6+6=0$ donc les deux vecteurs sont orthogonaux d'où les segments $[CE]$ et $[DF]$ sont perpendiculaires.
🔸 $CE=\sqrt{(-1,5)^2+(-4)^2}=\sqrt{18,25}$ et $DF=\sqrt{4^2+(-1,5)^2}=\sqrt{18,25}$ donc $CE=DF$