Problèmes du 1er et du second degré : Exercice 3 2ème année secondaire
Calcul dans IRProblèmes du 1er et du second degréNotion de polynômesArithmetiqueCalcul vectorielBarycentreTranslationsHomothetiesRotationsSuitesFonctionsTrigonométrieGéométrie analytiqueGéométrie dans l'espaceStatistiquesQCM
115 exercices
Exercice 3 --- (id : 77)
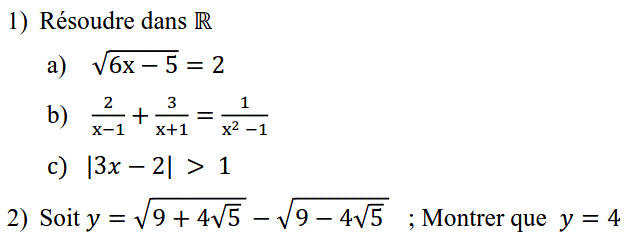
correction
1
a$\sqrt{6x-5}=2$ $\Longleftrightarrow 6x-5\geqslant 0$ et $6x-5=4$ $\Longleftrightarrow 6x=9$ et $x\geqslant \dfrac{5}{6}$ $\Longleftrightarrow x=\dfrac{9}{6}=\dfrac{3}{2}\geqslant \dfrac{5}{6}$ donc $\boxed{S_{\R}=\left\{{\dfrac{3}{2}}\right\}}$
b$\dfrac{2}{x-1}+\dfrac{3}{x+1}=\dfrac{1}{x^2-1}$ $\Longleftrightarrow 2(x+1)+3(x-1)=1$ et $x^2-1\neq 0$ $\Longleftrightarrow 5x-1=1$ et $(x-1)(x+1)\neq 0$ $\Longleftrightarrow x=\dfrac{2}{5}$ et $x\notin \left\{{-1;1}\right\}$ $\iff x=\dfrac{2}{5}$ donc $\boxed{S_{\R}=\left\{{\dfrac{2}{5}}\right\}}$
c$\left|{3x-2}\right|>1$ $\iff 3x-2>1\;ou\;3x-2<-1$ $\iff 3x>3\;ou\;3x< 1$ $\iff x>1\;ou\;x<\dfrac{1}{3}$ donc $\boxed{S_{\R}=\left]{-\infty;\dfrac{1}{3}}\right[\cup\left]{1;+\infty}\right[}$
2
$9\pm 4\sqrt{5}=4+5\pm 4\sqrt{5}$ $=(\sqrt{5})^2\pm 2\times 2\times \sqrt{5}+2^2$ $=\left({\sqrt{5}\pm 2}\right)^2$ $$\begin{align*} y&=\sqrt{9+4\sqrt{5}}-\sqrt{9-4\sqrt{5}}\\ &=\sqrt{\left({\sqrt{5}+2}\right)^2}-\sqrt{\left({\sqrt{5}-2}\right)^2}\\ &=\left|{\sqrt{5}+2}\right|-\left|{\sqrt{5}-2}\right|\\ &=\sqrt{5}+2-(\sqrt{5}-2)=4 \end{align*}$$
$9\pm 4\sqrt{5}=4+5\pm 4\sqrt{5}$ $=(\sqrt{5})^2\pm 2\times 2\times \sqrt{5}+2^2$ $=\left({\sqrt{5}\pm 2}\right)^2$ $$\begin{align*} y&=\sqrt{9+4\sqrt{5}}-\sqrt{9-4\sqrt{5}}\\ &=\sqrt{\left({\sqrt{5}+2}\right)^2}-\sqrt{\left({\sqrt{5}-2}\right)^2}\\ &=\left|{\sqrt{5}+2}\right|-\left|{\sqrt{5}-2}\right|\\ &=\sqrt{5}+2-(\sqrt{5}-2)=4 \end{align*}$$