Suites : Exercice 22 2ème année secondaire
Calcul dans IRProblèmes du 1er et du second degréNotion de polynômesArithmetiqueCalcul vectorielBarycentreTranslationsHomothetiesRotationsSuitesFonctionsTrigonométrieGéométrie analytiqueGéométrie dans l'espaceStatistiquesQCM
86 exercices
Exercice 22 --- (id : 557)
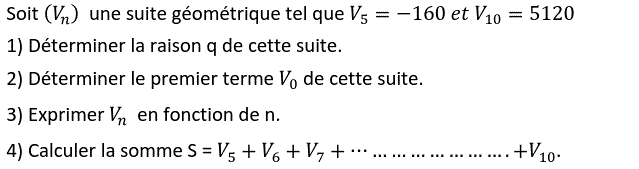
correction
$(V_n)$ est une suite géométrique telle que $V_5=-160$ et $V_{10}=5120$
1
$V_{10}=V_5q^{10-5}\iff V_{10}=V_5q^5$ $\iff q^5=\dfrac{V_{10}}{V_5}=\dfrac{5120}{-160}=-32$ $\iff q^5=(-2)^5 \iff \boxed{q=-2}$
2
$V_5=V_0q^5 \iff V_0=\dfrac{V_5}{q^5}$ $\iff V_0=\dfrac{-160}{(-2)^5}=\dfrac{-160}{-32}=5$
3
$V_n=V_0q^n$ $\iff V_n=5(-2)^n$
4
$S=V_5+V_6+V_7+...+V_{10}$ $=\sum\limits_{k=5}^{10}{V_k}=V_5\dfrac{1-q^{10-5+1}}{1-q}$ $\iff S=-160\times\dfrac{1-(-2)^6}{1-(-2)}$ $\iff S=160\times\dfrac{2^6-1}{3}$ $=160\times21=3360$