Fonctions : Exercice 1 2ème année secondaire
Calcul dans IRProblèmes du 1er et du second degréNotion de polynômesArithmetiqueCalcul vectorielBarycentreTranslationsHomothetiesRotationsSuitesFonctionsTrigonométrieGéométrie analytiqueGéométrie dans l'espaceStatistiquesQCM
61 exercices
Exercice 1 --- (id : 457)

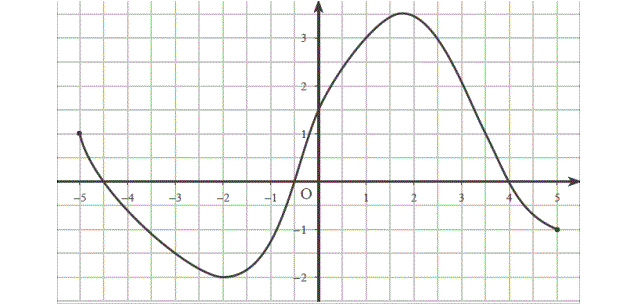
correction
1)
${D}_{f}=\left[{-5,5}\right]$
2)
$f(-3)=-\frac{3}{2} , f(0)=\frac{3}{2}$
3)
$f(x)=3\Leftrightarrow x=1$ ou $x=\frac{5}{2}$
4)
$$\def\arraystretch{2.2}\begin{array}{c|ccccccc}
x & -5 & & -2 & & \dfrac{7}{4} & & 5 \\ \hline
f(x) & 1 & \searrow & -2 & \nearrow & \dfrac{7}{2} & \searrow & -1
\end{array}$$
5)
a-
$f(x)=1 \Leftrightarrow x=-5$ ou $x=-\frac{1}{4}$ ou $x=\frac{7}{2}$
${S}_{\Bbb R}=\left\{{-5,-\frac{1}{4},\frac{7}{2}}\right\}$
${S}_{\Bbb R}=\left\{{-5,-\frac{1}{4},\frac{7}{2}}\right\}$
b-
$f(x)=-3$ impossible car $f(x) \in \left[{-2,\dfrac{7}{2}}\right]$
${S}_{\Bbb R}=\varnothing$
${S}_{\Bbb R}=\varnothing$
c-
$f(x)<6 \Leftrightarrow x \in \left[{-2,\dfrac{7}{2}}\right]$
${S}_{\Bbb R}=\left[{-2,\dfrac{7}{2}}\right]$
${S}_{\Bbb R}=\left[{-2,\dfrac{7}{2}}\right]$