Activités numériques II : Exercice 9 première année secondaire
Activités numériques IActivités numériques IIActivités algébriquesFonctions linéairesEquations et inéquationsFonctions affinesSystème de deux équationsStatistiquesAnglesThalesRapports trigonométriqueVecteurs et translationsActivités dans un repereQuart de tourSections planes solideQCM
119 exercices
Exercice 9 --- (id : 1192)
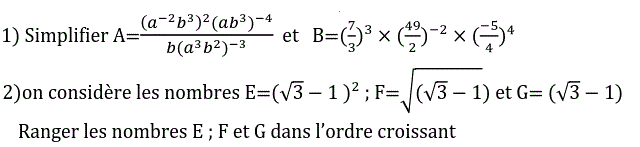
correction
1)
$$\begin{align*}
A&=\frac{\left({a^{-2}b^3}\right)^{2}\left({ab^3}\right)^{-4}}{b\left({a^3b^2}\right)^{-3}} \\
&=\frac{a^{-4}b^6a^{-4}b^{-12}}{ba^{-9}b^{-6}}=\frac{a^{-8}b^{-6}}{a^{-9}b^{-5}} \\
&=a^{-8+9}b^{-6+5}=ab^{-1}=\frac{a}{b}\\
B&=\left({\frac{7}{3}}\right)^{3}\times \left({\frac{49}{2}}\right)^{-2}\times \left({\frac{-5}{4}}\right)^4 \\
&=\frac{7^3}{3^3}\times \frac{\left({7^2}\right)^{-2}}{2^{-2}}\times\frac{\left({-5}\right)^4}{\left({2^2}\right)^4} \\
&=\frac{7^3\times7^{-4}\times 5^4}{3^3\times 2^{-2}\times 2^8}=\frac{7^{-1}\times 5^4}{3^3\times 2^6}\\
&=\frac{5^4}{2^6\times 3^3\times 7}=\frac{625}{12096}
\end{align*}$$
2)
On sait que pour tout réel positif a compris entre 0 et 1 on a: $a^2\leqslant a \leqslant \sqrt{a}$
Or $\sqrt{3}-1\approx 0,7$ donc $\sqrt{3}-1$ est un réel positif compris entre 0 et 1
Donc d'après l'encadrement précédent on peut remplacer a par $\sqrt{3}-1$ on obtient alors:
$\left({\sqrt{3}-1}\right)^2\leqslant \sqrt{3}-1\leqslant \sqrt{\sqrt{3}-1}$
Donc $E\leqslant G \leqslant F$
Or $\sqrt{3}-1\approx 0,7$ donc $\sqrt{3}-1$ est un réel positif compris entre 0 et 1
Donc d'après l'encadrement précédent on peut remplacer a par $\sqrt{3}-1$ on obtient alors:
$\left({\sqrt{3}-1}\right)^2\leqslant \sqrt{3}-1\leqslant \sqrt{\sqrt{3}-1}$
Donc $E\leqslant G \leqslant F$