Activités numériques II : Exercice 6 première année secondaire
Activités numériques IActivités numériques IIActivités algébriquesFonctions linéairesEquations et inéquationsFonctions affinesSystème de deux équationsStatistiquesAnglesThalesRapports trigonométriqueVecteurs et translationsActivités dans un repereQuart de tourSections planes solideQCM
119 exercices
Exercice 6 --- (id : 1242)
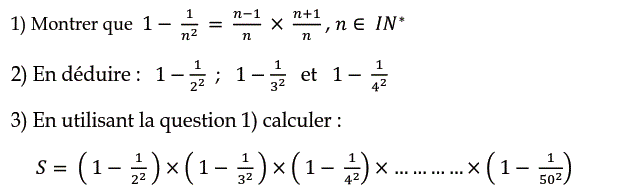
correction
1)
$$\begin{align*}
1-\frac{1}{n^2}&=\frac{n^2}{n^2}-\frac{1}{n^2} \\[0.5em]
&=\frac{n^2-1}{n^2} \\[0.5em]
&=\frac{(n-1)\times(n+1)}{n \times n} \\[0.5em]
&=\frac{n-1}{n} \times \frac{n+1}{n}
\end{align*}$$
2)
Appliquons la formule précédente
🔶Pour $n=2$ on obtient :
$1-\dfrac{1}{2^2}=\dfrac{1}{2}\times \dfrac{3}{2}$
🔶Pour $n=3$ on obtient :
$1-\dfrac{1}{3^2}=\dfrac{2}{3}\times \dfrac{4}{3}$
🔶Pour $n=4$ on obtient :
$1-\dfrac{1}{4^2}=\dfrac{3}{4}\times \dfrac{5}{4}$
🔶Pour $n=2$ on obtient :
$1-\dfrac{1}{2^2}=\dfrac{1}{2}\times \dfrac{3}{2}$
🔶Pour $n=3$ on obtient :
$1-\dfrac{1}{3^2}=\dfrac{2}{3}\times \dfrac{4}{3}$
🔶Pour $n=4$ on obtient :
$1-\dfrac{1}{4^2}=\dfrac{3}{4}\times \dfrac{5}{4}$
3)
$$\begin{align*}
S=&\left({1-\frac{1}{2^2}}\right)\times\left({1-\frac{1}{3^2}}\right)\times\left({1-\frac{1}{4^2}}\right)\times...\times\left({1-\frac{1}{50^2}}\right) \\
&=\frac{1}{2}\times \frac{3}{2} \times \frac{2}{3}\times \frac{4}{3}\times \frac{3}{4}\times \frac{5}{4}\times ... \times \frac{49}{50}\times \frac{51}{50} \end{align*}$$
Après simplifications on obtient :
$S=\dfrac{1}{2}\times \dfrac{51}{50}=\dfrac{51}{100}$
$S=\dfrac{1}{2}\times \dfrac{51}{50}=\dfrac{51}{100}$