Equations et inéquations : Exercice 31 première année secondaire
Activités numériques IActivités numériques IIActivités algébriquesFonctions linéairesEquations et inéquationsFonctions affinesSystème de deux équationsStatistiquesAnglesThalesRapports trigonométriqueVecteurs et translationsActivités dans un repereQuart de tourSections planes solideQCM
81 exercices
Exercice 31 --- (id : 1602)
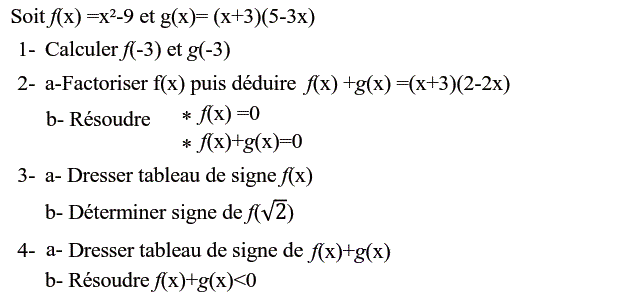
correction
Soit $f(x)=x^2-9$ et $g(x)=(x+3)(5-3x)$
1-
🌻$f(-3)=(-3)^2-9=9-9=0$
🌻$g(-3)=(-3+3)(5-3\times(-3))$ $=0\times 14=0$
🌻$f(-3)=(-3)^2-9=9-9=0$
🌻$g(-3)=(-3+3)(5-3\times(-3))$ $=0\times 14=0$
2-
a-
🌻$f(x)=x^2-9=x^2-3^2$ $=(x-3)(x+3)$
🌻$f(x)+g(x)$
$=(x-3)(x+3)+(x+3)(5-3x)$
$=(x+3)[(x-3)+(5-3x)]$
$=(x+3)(x-3+5-3x)$
$=(x+3)(2-2x)$
🌻$f(x)+g(x)$
$=(x-3)(x+3)+(x+3)(5-3x)$
$=(x+3)[(x-3)+(5-3x)]$
$=(x+3)(x-3+5-3x)$
$=(x+3)(2-2x)$
b-
🌻$f(x)=0$
$\iff (x-3)(x+3)=0$
$\iff x-3=0$ ou $x+3=0$
$\iff x=3\; ou\; x=-3$
🌻$f(x)+g(x)=0$
$\iff (x+3)(2-2x)=0$
$\iff x+3=0 \; ou \; 2-2x=0$
$\iff x=-3 \; ou \; -2x=-2$
$\iff x=-3 \; ou \; x=1$
$\iff (x-3)(x+3)=0$
$\iff x-3=0$ ou $x+3=0$
$\iff x=3\; ou\; x=-3$
🌻$f(x)+g(x)=0$
$\iff (x+3)(2-2x)=0$
$\iff x+3=0 \; ou \; 2-2x=0$
$\iff x=-3 \; ou \; -2x=-2$
$\iff x=-3 \; ou \; x=1$
3-
a-
$$\small \begin{array}{|c|ccccccc|}
\hline
x & -\infty & & -3 & & 3 & & +\infty \\ \hline
x+3 & & - & 0 & + & & + \\ \hline
x-3 & & - & & - & 0 & + \\ \hline
f(x) & & + & 0 & - & 0 & + \\ \hline
\end{array}$$
b-
$\sqrt 2\in \left]{-3;3}\right[$ donc $f(\sqrt 2)<0$ (voir tableau de signe)
4-
a-
$$\small \begin{array}{|c|ccccccc|}
\hline
x & -\infty & & -3 & & 1 & & +\infty \\ \hline
x+3 & & - & 0 & + & & + \\ \hline
2-2x & & + & & + & 0 & - \\ \hline
f(x)+g(x) & & - & 0 & + & 0 & - \\ \hline
\end{array}$$
b-D'après le tableau de signe précédent on a :
$f(x)+g(x)<0$ $\iff x\in \left]{-\infty;-3}\right[\cup \left]{1;+\infty}\right[$
Donc $\boxed{S_\Bbb R=\left]{-\infty;-3}\right[\cup \left]{1;+\infty}\right[}$
Donc $\boxed{S_\Bbb R=\left]{-\infty;-3}\right[\cup \left]{1;+\infty}\right[}$