Equations et inéquations : Exercice 2 première année secondaire
Activités numériques IActivités numériques IIActivités algébriquesFonctions linéairesEquations et inéquationsFonctions affinesSystème de deux équationsStatistiquesAnglesThalesRapports trigonométriqueVecteurs et translationsActivités dans un repereQuart de tourSections planes solideQCM
81 exercices
Exercice 2 --- (id : 1474)
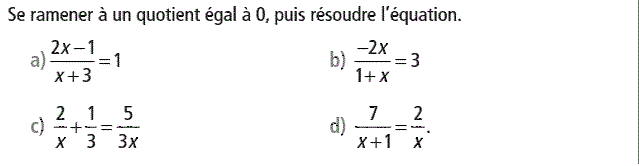
correction
pour chacune des équations suivantes, on désigne par S son ensemble de solutions.
a)
$$\begin{align*}
&\frac{2x-1}{x+3}=1 \\
&\text{équivaut}\;\; \frac{2x-1}{x+3}-1=0 \\
&\text{équivaut}\;\; \frac{2x-1}{x+3}-\frac{x+3}{x+3}=0 \\
&\text{équivaut}\;\; \frac{(2x-1)-(x+3)}{x+3}=0 \\
&\text{équivaut}\;\; \frac{2x-1-x-3}{x+3}=0 \\
&\text{équivaut}\;\; \frac{x-4}{x+3} \\
&\text{équivaut}\;\; x-4=0\; et \;x+3\neq 0 \\
&\text{équivaut}\;\; x=4
\end{align*}$$
Donc $S=\boxed{\left\{{4}\right\}}$
b)
$$\begin{align*}
&\frac{-2x}{1+x}=3 \\
&\text{équivaut}\;\; \frac{-2x}{1+x}-3=0 \\
&\text{équivaut}\;\; \frac{-2x}{1+x}-\frac{3(1+x)} {1+x}=0 \\
&\text{équivaut}\;\; \frac{-2x-3(1+x)}{1+x}=0 \\
&\text{équivaut}\;\; \frac{-2x-3-3x}{1+x}=0 \\
&\text{équivaut}\;\; \frac{-5x-3}{1+x}=0 \\
&\text{équivaut}\;\; -5x-3=0\; et \; x+1\neq 0 \\
&\text{équivaut}\;\; x=-\frac{3}{5}
\end{align*}$$
Donc $\boxed{S=\left\{{-\frac{3}{5}}\right\} }$
c)
$$\begin{align*}
&\frac{2}{x}+\frac{1}{3}=\frac{5}{3x} \\
&\text{équivaut}\;\; \frac{6}{3x}+\frac{x}{3x}-\frac{5}{3x}=0 \\
&\text{équivaut}\;\; \frac{6+x-5}{3x}=0 \\
&\text{équivaut}\;\; \frac{1+x}{3x}=0 \\
&\text{équivaut}\;\; 1+x=0\; et \;3x\neq 0 \\
&\text{équivaut}\;\; x=-1\; et \; x\neq 0 \\
&\text{équivaut}\;\; x=-1
\end{align*}$$
Donc $\boxed{S=\left\{{-1}\right\} }$
d)
$$\begin{align*}
&\frac{7}{x+1}=\frac{2}{x} \\
&\text{équivaut}\;\; \frac{7x}{x(x+1)}-\frac{2(x+1)}{x(x+1)}=0 \\
&\text{équivaut}\;\; \frac{7x-2(x+1)}{x(x+1)}=0 \\
&\text{équivaut}\;\; \frac{7x-2x-2}{x(x+1)}=0 \\
&\text{équivaut}\;\; \frac{5x-2}{x(x+1)}=0 \\
&\text{équivaut}\;\; 5x-2=0\; et \;x(x+1)\neq 0 \\
&\text{équivaut}\;\; x=\frac{2}{5}\; et \; (x\neq 0\; et \;x\neq -1)
\end{align*}$$
Donc $\boxed{S=\left\{{\frac{2}{5}}\right\} }$