Fonctions linéaires : Exercice 18 première année secondaire
Activités numériques IActivités numériques IIActivités algébriquesFonctions linéairesEquations et inéquationsFonctions affinesSystème de deux équationsStatistiquesAnglesThalesRapports trigonométriqueVecteurs et translationsActivités dans un repereQuart de tourSections planes solideQCM
54 exercices
Exercice 18 --- (id : 1619)

correction
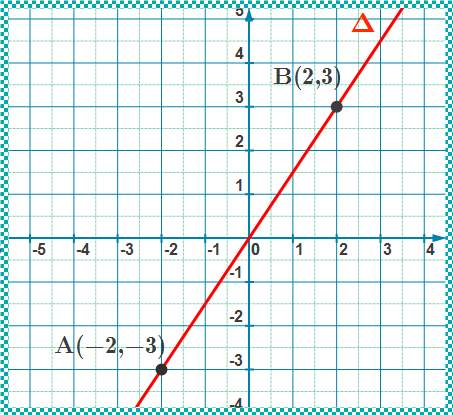
1°)
On a $f(0)=0$ et $f(2)=\dfrac{3}{2}\times 2=3$ donc $\Delta$ passe par les points $O(0,0)$ et $B(2,3)$
2°)
$f(-2)=\dfrac{3}{2}\times (-2)=-3$ donc le point $A(-2,-3)\in \Delta$
3°)
$O \in \Delta$ et $A\in \Delta$ donc les points O, A et M sont alignés équivaut $M\in \Delta$
$M(t-1,t+1)\in \Delta$
équivaut $f(t-1)=t+1$
équivaut $\dfrac{3}{2}(t-1)=t+1$
équivaut $\dfrac{3}{2}t-\dfrac{3}{2}=t+1$
équivaut $\dfrac{3}{2}t-t=1+\dfrac{3}{2}$
équivaut $\left({\dfrac{3}{2}-1}\right)t=\dfrac{5}{2}$
équivaut $\dfrac{1}{2}t=\dfrac{5}{2}$
équivaut $t=5$
$M(t-1,t+1)\in \Delta$
équivaut $f(t-1)=t+1$
équivaut $\dfrac{3}{2}(t-1)=t+1$
équivaut $\dfrac{3}{2}t-\dfrac{3}{2}=t+1$
équivaut $\dfrac{3}{2}t-t=1+\dfrac{3}{2}$
équivaut $\left({\dfrac{3}{2}-1}\right)t=\dfrac{5}{2}$
équivaut $\dfrac{1}{2}t=\dfrac{5}{2}$
équivaut $t=5$