Activités numériques II : Exercice 1 première année secondaire
Activités numériques IActivités numériques IIActivités algébriquesFonctions linéairesEquations et inéquationsFonctions affinesSystème de deux équationsStatistiquesAnglesThalesRapports trigonométriqueVecteurs et translationsActivités dans un repereQuart de tourSections planes solideQCM
119 exercices
Exercice 1 --- (id : 999)
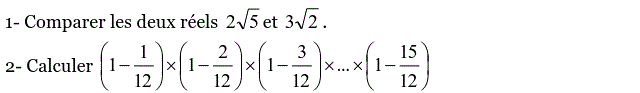
correction
1)
✎
$\left({2\sqrt 5}\right)^2=4\times 5=20$ et $\left({3\sqrt 2}\right)^2=9\times 2=18$
$\left({3\sqrt 2}\right)^2=18< \left({2\sqrt 5}\right)^2=20$ donc $3\sqrt 2<2 \sqrt 5$
$\left({3\sqrt 2}\right)^2=18< \left({2\sqrt 5}\right)^2=20$ donc $3\sqrt 2<2 \sqrt 5$
2)
✎
$\left({1-\frac{1}{12}}\right)\times \left({1-\frac{2}{12}}\right)\times ...\times \left({1-\frac{15}{12}}\right)$
Les facteurs de ce produit sont de la forme $1-\frac{n}{12}$ où $n\in \left\{{1,2,...,15}\right\}$
Donc $1-\frac{12}{12}=0$ est l'un de ces facteurs d'où ce produit est nul.
Les facteurs de ce produit sont de la forme $1-\frac{n}{12}$ où $n\in \left\{{1,2,...,15}\right\}$
Donc $1-\frac{12}{12}=0$ est l'un de ces facteurs d'où ce produit est nul.